爆笑解法:
【问题描述】
鸡、兔同笼,共有头10个,足30只,求兔子有多少只?
【爆笑解法】
假设鸡和兔子皆训练有素,
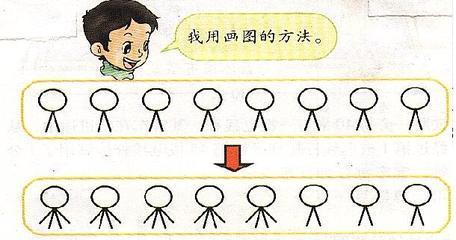
吹一声哨,鸡和兔子都抬起一只脚,地上站着30-10=20条腿,鸡肯定都金鸡独立,兔儿则成了三脚猫;
再吹哨,地上只站着20-10=10条腿,这时鸡一屁股坐地上了,兔子则两只脚着地,进化为直立行走,兔子共有10÷2=5只,而鸡有10-5=5只。
此种算法,让二元一次方程情何以堪……
附:鸡兔同笼的其他解法
鸡兔同笼问题是我国古代著名趣题之一。通过学习解鸡兔同笼问题,可以提高我们的分析问题、解决问题的能力。下面我来介绍几种解鸡兔同笼问题的方法:
【例题】
大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题,这就是著名的“鸡兔同笼”问题。书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”意思就是:笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94只脚,问鸡和兔各有多少只?
【解法一:列表枚举法】
列表枚举法就是让我们列出表格,采用依次列举,逐步尝试的方法来解决这个问题。详细过程见下表:
鸡 35 34 33 32 …… 26 25 24 23 兔 0 1 2 3 …… 9 10 11 12 脚 70 72 74 76 …… 88 90 92 94用这种方法解题简单,容易理解,但过程太过笨拙、繁琐,相信它也不符合你的口味儿吧!
【解法二:抬腿法】
这是古人解题的方法,也就是《孙子算经》中采用的方法。
1、抬腿,即鸡“金鸡独立”,兔两个后腿着地,前腿抬起,腿的数量就为原来数量的一半。94÷2=47只脚。
2、现在鸡有一只脚,兔有两只脚。笼子里只要有一只兔子,脚数就比头数多1。
3、那么脚数与头数的差47-35=12就是兔子的只数。
4、最后用头数减去兔的只数35-12=23就得出鸡的只数。
所以,我们可以总结出这样的公式:兔子的只数=总腿数÷2-总只数。
【解法三:假设法】
假设法是鸡兔同笼类问题最常用的方法之一。假设这35个头都是兔子,那么腿数就应该是35×4=140,就比94还多,那么是哪里多的呢?当然是我们把两条腿的鸡看成了四条腿的兔子了。我们都知道一只兔子比一只鸡多2条腿,多2条腿就有1只鸡,那么多的腿数当中有多少个2就有多少只鸡。我们可以列式为:鸡的只数=(35×4-94)÷(4-2)。总结公式为:鸡的只数=(兔的脚数×总只数-总腿数)÷(兔的腿数-鸡的腿数)。
当然我们也可以把这35个头都看成鸡的,那么腿数应该是35×2=70,就比94还少,相信不说你也明白为什么少了?对,因为我们把4条腿的兔子看成了2条腿的鸡,那么每少两条腿就有1只兔子。所以我们可以这样列式:兔的只数=(94-35×2)÷(4-2)。总结公式为:兔的只数=(总脚数-鸡的脚数×总只数)÷(兔的脚数-鸡的脚数)。
 爱华网
爱华网