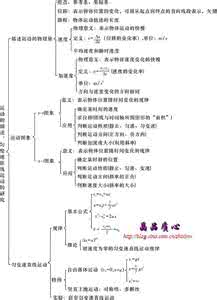
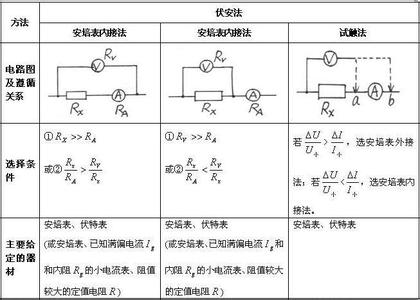
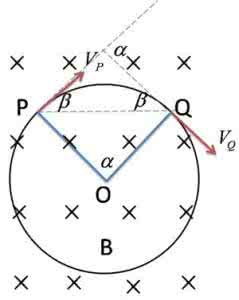
【考点自清】
一、两类动力学问题
牛顿第二定律确定了运动和力的关系,使我们能够把物体的受力情况与运动情况联系起来。
利用牛顿第二定律解决动力学问题的关键是利用加速度的“桥梁”作用,将运动学规律和牛顿第二定律相结合,寻找加速度和未知量的关系,是解决这类问题的思考方向。
1、已知受力情况求运动情况
已知物体的受力情况,根据牛顿第二定律,可以求出物体的运动情况;已知物体的初始条件(初位置和初速度),根据运动学公式,就可以求出物体在任一时刻的速度和位移,也就可以求解物体的运动情况。
可用程序图表示如下:
2、已知物体的运动情况求物体的受力情况
根据物体的运动情况,由运动学公式可以求出加速度,再根据牛顿第二定律可确定物体的受力情况,从而求出未知的力,或与力相关的某些物理量。如动摩擦因数、劲度系数、力的方向等。
可用程序图表示如下:
二、解答两类动力学问题的基本方法及步骤
1.基本方法
⑴明确题目中给出的物理现象和物理过程的特点,如果是比较复杂的问题,应该明确整个物理现象是由几个物理过程组成的,找出相邻过程的联系点,再分别研究每一个物理过程.
⑵根据问题的要求和计算方法,确定研究对象,进行分析,并画出示意图.图中应注明力、速度、加速度的符号和方向.对每一个力都应明确施力物体和受力物体,以免分析力时有所遗漏或无中生有.
⑶应用牛顿运动定律和运动学公式求解,通常先用表示物理量的符号运算,解出所求物理量的表达式来,然后将已知物理量的数值及单位代入,通过运算求结果.应事先将已知物理量的单位都统一采用国际单位制中的单位.
⑷分析流程图
两类基本问题中,受力分析是关键,求解加速度是桥梁和枢纽,思维过程如下:
2、应用牛顿第二定律的解题步骤
(1)明确研究对象。根据问题的需要和解题的方便,选出被研究的物体。
(2)分析物体的受力情况和运动情况,画好受力分析图,明确物体的运动性质和运动过程。
(3)选取正方向或建立坐标系,通常以加速度的方向为正方向或以加速度方向为某一坐标轴的正方向。
(4)求合外力F合。
(5)根据牛顿第二定律F合=ma列方程求解,必要时还要对结果进行讨论。
特别提醒:
①物体的运动情况是由所受的力及物体运动的初始状态共同决定的。
②无论是哪种情况,联系力和运动的“桥梁”是加速度。
【重点精析】
一、动力学基本问题分析
【例1】风洞实验中可产生水平方向的、大小可以调节的风力,先将一套有小球的细杆放入风洞实验室,小球孔径略大于细杆直径,如图所示。
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上匀速运动,这时所受风力为小球所受重力的0.5倍,求小球与杆的动摩擦因数;
(2)保持小球所受风力不变,使杆与水平方向间夹角为37°并固定,则小球从静止出发在细杆上滑下距离x的时间为多少。(sin 37°=0.6,cos 37°=0.8)
【变式练习1】如右图所示,质量M=10kg的木楔ABC静置于粗糙水平地面上,滑动摩擦系数μ=0.02.在木楔的倾角θ=30°的斜面上,有一质量m=1.0kg的物块由静止开始沿斜面下滑.当滑行位移s=1.4m时,其速度v=1.4m/s。在这过程中木楔没有滑动,求地面对木楔的静摩擦力的大小和方向以及地面对木楔的支持力(取g=10m/s2).
【互动探究】字母演算最后为Mg+mg+masinθ,又说明了什么呢?
二、多过程问题分析
复杂过程的处理方法——程序法
按时间的先后顺序对题目给出的物体运动过程(或不同的状态)进行分析(包括列式计算)的解题方法可称为程序法。用程序法解题的基本思路是:
1、划分出题目中有多少个不同的过程或多少个不同的状态。
2、对各个过程或各个状态进行具体分析,得出正确的结果。
3、前一个过程的结束就是后一个过程的开始,两个过程的分界点是关键。
【例2】质量m=30 kg的电动自行车,在F=180 N的水平向左的牵引力的作用下,沿水平面从静止开始运动.自行车运动中受到的摩擦力F′=150 N.在开始运动后的第5 s末撤消牵引力F.求从开始运动到最后停止电动自行车总共通过的路程.
【变式练习2】一辆汽车在恒定牵引力作用下由静止开始沿直线运动,4 s内通过8 m的距离,此后关闭发动机,汽车又运动了2 s停止,已知汽车的质量m=2×103 kg,汽车运动过程中所受阻力大小不变,求:
(1)关闭发动机时汽车的速度大小;
(2)汽车运动过程中所受到的阻力大小;
(3)汽车牵引力的大小.
【例3】质量为m=2kg的木块原来静止在粗糙水平地面上,现在第1、3、5……奇数秒内给物体施加方向向右、大小为F1=6N的水平推力,在第2、4、6……偶数秒内给物体施加方向仍向右、大小为F2=2N的水平推力。已知物体与地面间的动摩擦因数μ=0.1,取g=10m/s2,问:
(1)木块在奇数秒和偶数秒内各做什么运动?
(2)经过多长时间,木块位移的大小等于40.25m?
说明:(1)本题属于已知受力情况求运动情况的问题,解题思路为先根据受力情况由牛顿第二定律求加速度,再根据运动规律求运动情况.
(2)根据物体的受力特点,分析物体在各段时间内的运动情况,并找出位移的一般规律,是求解本题的关键.
三、“等时圆”模型的基本规律及应用
1、等时圆模型(如图所示)
2、等时圆规律:
⑴小球从圆的顶端沿光滑弦轨道静止滑下,滑到弦轨道与圆的交点的时间相等。(如图a)
⑵小球从圆上的各个位置沿光滑弦轨道静止滑下,滑到圆的底端的时间相等。(如图b)
⑶沿不同的弦轨道运动的时间相等,都等于小球沿竖直直径(d)自由落体的时间,即
3、等时性的证明
设某一条弦与水平方向的夹角为α,圆的直径为d(如右图)。根据物体沿光滑弦作初速度为零的匀加速直线运动,加速度为a=gsinα,位移为s=dsinα,所以运动时间为
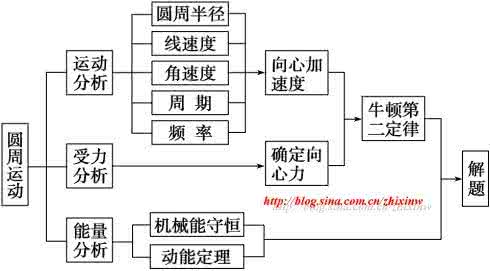
即沿各条弦运动具有等时性,运动时间与弦的倾角、长短无关。
【例4】如图,通过空间任一点A可作无限多个斜面,若将若干个小物体从点A分别沿这些倾角各不相同的光滑斜面同时滑下,那么在同一时刻这些小物体所在位置所构成的面是( )
A.球面 B.抛物面 C.水平面 D.无法确定
【解析】由“等时圆”可知,同一时刻这些小物体应在同一“等时圆”上,所以A正确。
【变式练习3】如图,位于竖直平面内的固定光滑圆轨道与水平面相切于M点,与竖直墙相切于点A,竖直墙上另一点B与M的连线和水平面的夹角为600,C是圆环轨道的圆心,D是圆环上与M靠得很近的一点(DM远小于CM)。已知在同一时刻:a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道运动到M点;c球由C点自由下落到M点;d球从D点静止出发沿圆环运动到M点。则( )
A.a球最先到达M点 B.b球最先到达M点
C.c球最先到达M点 D.d球最先到达M点
【例4】如图a所示,在同一竖直线上有A、B两点,相距为h,B点离地高度为H,现在要在地面上寻找一点P,使得从A、B两点分别向点P安放的光滑木板,满足物体从静止开始分别由A和B沿木板下滑到P点的时间相等,求O、P两点之间的距离。
【变式练习4】如图是一倾角为α的输送带,A处为原料输入口,为避免粉尘飞扬,在A与输送带间建立一管道(假使光滑),使原料从A处以最短的时间到达输送带上,则管道与竖直方向的夹角应为多大?
【同步作业】
1、静止在水平地面上的物体的质量为2 kg,在水平恒力F推动下开始运动,4 s末它的速度达到4 m/s,此时将F撤去,又经6 s物体停下来,如果物体与地面的动摩擦因数不变,求F的大小。
2、消防队员为缩短下楼的时间,往往抱着竖直的杆直接滑下.假设一名质量为60kg、训练有素的消防队员从七楼(即离地面18m的高度)抱着竖直的杆以最短的时间滑下.已知杆的质量为200kg,消防队员着地的速度不能大于6m/s,手和腿对杆的最大压力为1800N,手和腿与杆之间的动摩擦因数为0.5,设当地的重力加速度 g=10m/s2.假设杆是固定在地面上的,杆在水平方向不移动.试求:
(1)消防队员下滑过程中的最大速度;
(2)消防队员下滑过程中杆对地面的最大压力;
(3)消防队员下滑的最短的时间.
 爱华网
爱华网