Bo'erziman fangcheng shuzhi jiefa
玻耳兹曼方程数值解法
numerical method for Boltzmann equations
玻耳兹曼方程是原子物理、天体物理等领域中的描写粒子(中子、质子、光子等)运动的基本微分-积分方程。假定粒子在两次碰撞之间作等速直线运动,而在穿过介质的过程中按照一定的概率与其他粒子相碰撞,从而发生偏斜、慢化、被吸收或增殖等现象。由于粒子是大量的,因此可以忽略统计起伏,把它们看成是连续体。求解玻耳兹曼方程,就是要求出在任一时刻,具有不同速度的粒子在空间的分布。玻耳兹曼方程数值解法很多,其中以解描述中子输运问题的玻耳兹曼方程的数值方法较为典型。
描述非定常中子输运过程的玻耳兹曼方程为:
[28-1], (1)式中为时间;r、分别为中子的位置和速度向量,=Ω,Ω为中子速度方向的单位向量;(r,,)为中子角通量分布;(,r)表示在点r处速度为的中子的宏观总截面,=(,r);(→;r)d是在r处中子速度由转移到与+d[kg2]之间的总概率;[285-500]是独立中子源。对于单速各向同性散射一维球对称问题,非定常中子输运方程为
[28-2]式中为径向坐标;[kg2]=cos,为向径和速度向量间的夹角;()为总截面;()=()(),()为在处每次碰撞所产生的平均次级中子数方程(2)的定解条件为
[28-3]
[28-5]。
20世纪40年代发展了用于解定常问题的两类主要解法。
①球谐函数法 它把和[285-500]按勒让德多项式()(球谐函数)展开,例如,令
[28-6]利用勒让德多项式的性质,把方程简化,再取展式的前+1项,得,,…,的+1个方程的联立方程组,然后用差分法求数值解。该法又称为P近似法。
②威克-昌德拉塞卡离散纵标法 简称WC法它(主要针对平板几何问题)是取的一组固定值,,,…,,对(,,)(=1,2,…,)写出方程组。右端积分用数值积分逼近,例如取为勒让德多项式零点的高斯求积公式,然后用差分法求解。对于各向同性散射的平板问题,WC法和球谐函数法是等价的。
1953年 B.G.卡尔森提出了解中子输运方程(2)的方法,该法取-1==1(其中[29-1][29-2]),把[-1,1]分成个区间,在每个区间[-1,]上假定是的线性函数,同样取[29-3],假定在每个区间 [-1,]上 也是 的线性函数。将(2)在区域{-1,-1}上对和积分,然后对时间作隐式向后差分得到差分格式,并适当选取插值公式,使差分方程的解满足粒子数守恒的性质。
卡尔森等人在50年代末进一步提出离散法,又称
离散纵标法(简记DSN法)。这种方法可以比较容易地推广到多维情况。它是从守恒方程
[29-5] 出发的,离散分点取为 [29-6],-1,,…,取为勒让德多项式零点,取为偶数,右端积分用高斯积分公式近似。在点[29-7]上建立差分,为此在高斯积分系数对应的子区间上对 近似积分,在(-1,)上对作体积分,对用中心差分,则得
[29-8]式中[29-9]是以 -1和为内外半径的球壳的体积,A是半径为的球面面积。
[29-10],[29-11]按递推公式
[29-12]求出。此外,还要补充关系
[29-13]和边界(=-1)方程
[29-14] 定解条件离散化为 [29-15][29-16]。若取为迭代初值,把中的用前次迭代值代入,则利用边界条件,(4)、(5)可显式递推求解,计算步骤按从小到大的顺序进行。当从大到小进行计算,当>0时,则利用中心对称条件,对从小到大进行计算。
方法和 DSN方法是求解玻耳兹曼方程的有效的数值方法,其主要缺点是计算中可能出现负通量,为了避免出现负通量有各种修正格式。
对于定常的玻耳兹曼方程,70年代出现了多种有限元算法。有通过引进角通量偶次分量,把方程化为自伴形式,再构造泛函求极小的有限元算法;也有直接用加廖金法(包括连续的和不连续的方法)和配置法等的有限元算法。
此外,还有许多其他的数值方法,例如特征线法、分裂法和几种方法相结合的混合解法,以及求解积分型输运方程的各种数值方法。而基本概率理论的蒙特卡罗法在输运计算中也占有重要的地位。
参考书目
R. D. Richtmyer and K. W. Morton, Difference Method for Initialvalue Problems , 2nded.,Interscience, New York,1967.
杜明笙
以上就是网友分享的关于"玻耳兹曼方程数值解法"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
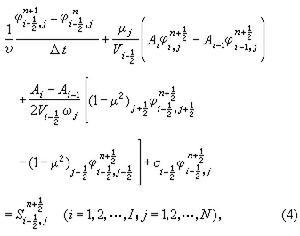
 爱华网
爱华网