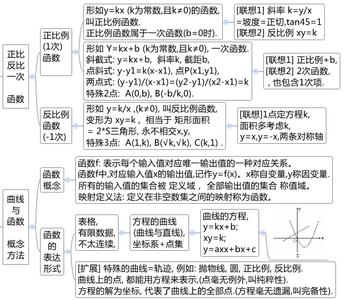
21、据报道,我省农作物秸杆的资源巨大,但合理利用量十分有限,2006年的利用率只有30%,大部分秸杆被直接焚烧了,假定我省每年产出的农作物秸杆总量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%,求每年的增长率.(取 2≈1.41)
本题中可设我省每年产出的农作物秸杆总量为a,合理利用量的增长率是x,06年的利用量是30%a,那么07年的利用率就是30%(1+x),08年的利用量就是30%a(1+x)2,进而可列出方程,求出答案.
解答:解:设我省每年产出的农作物秸杆总量为a,合理利用量的增长率是x,由题意得
30%a(1+x)2=60%a,
即(1+x)2=2(5分)
∴x1≈0.41,x2≈-2.41(不合题意舍去).(7分)
∴x≈0.41.
答:每年的增长率约为41%.(8分)
22、下面的四个结论,回答问题.
①x2-3x+2=0的两根为x1=1,x2=2;
②(x-1)(x-2)=0的两根为x1=1,x2=2;
③(x-1)(x-2)=x2-3x+2;
④二次三项式x2-3x+2可分解为(x-1)(x-2).
猜测
若关于x的方程x2+px+q=0的两根为x1=3,x2=-4,则二次三项式x2+px+q可分解为
.
应用在实数范围内分解因式:
(1)2x2-4x+2
(2) 13x2-23x-1
(3)x2-2x-2
猜测:若关于x的方程x2+px+q=0的两根为x1,x2,那么x2+px+q=(x-x1)(x-x2),把所求得的解代入即可;
(1)提取公因式2后用完全平方公式分解即可;
(2)求得方程的相应解为x1,x2,则ax2+px+q=a(x-x1)(x-x2),把所求得的解代入即可;
(3)求得方程的相应解为x1,x2,则x2+px+q=(x-x1)(x-x2),把所求得的解代入即可.
解:猜测:(x-3)(x+4)(2分);
应用:(1)原式=2(x2-2x+1)(4分)
=2(x-1)2(5分);
(2)原式= 13(x2-2x-3).(7分)
= 13(x-3)(x+1)(8分);
(3)设x2-2x-2=0,解这个方程得其解为 x=1±3(10分);
∴x2-2x-2= (x-1-3)(x-1+3).(12分)
考查知识点为:若方程ax2+px+q=0的两根为x1,x2,则ax2+px+q=a(x-x1)(x-x2).
28、今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;
(2)若小红家有4人,明年小红家减少多少农业税?
(3)小红所在的乡约有16000农民,问该乡农民明年减少多少农业税?
(1) 设设降低的百分率为x,则降低一次后的数额是25(1-x),再在这个数的基础上降低x,则变成25(1-x)(1-x)即25(1-x)2,据此即可列方程求解;
(2)每人减少的税额是25x,则4个人的就是4×25x,代入(1)中求得的x的值,即可求解;
(3)每个人减少的税额是25x,乘以总人数16000即可求解.
解:(1)设降低的百分率为x,依题意有,25(1-x)2=16,
解得,x1=0.2=20%,x2=1.8(舍去);
(2)小红全家少上缴税25×20%×4=20(元);
(3)全乡少上缴税16000×25×20%=80 000(元).
答:降低的增长率是20%,明年小红家减少的农业税是20元,该乡农民明年减少的农业税是80 000元.
点评:本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.
22、顾客李某于今年“五•一”期间到电器商场购买空调,与营业员有如下的一段对话:
顾客李某:A品牌的空调去年“国庆”期间价格还挺高,这次便宜多了,一次降价幅度就达到19%,是不是质量有问题
营业员:不是一次降价,这是第二次降价,今年春节期间已经降了一次价,两次降价的幅度相同.我们所销售的空调质量都是很好的,尤其是A品牌系列空调的质量是一流的.
顾客李某:我们单位的同事也想买A品牌的空调,有优惠政策吗?
营业员:有,请看《购买A品牌系列空调的优惠办法》.
购买A品牌系列空调的优惠办法:
方案一:各种型号的空调每台价格优惠5%,送货上门,负责安装,每台空调另加运输费和安装费共90元.
方案二:各种型号的空调每台价格优惠2%,送货上门,负责安装,免运输费和安装费.
根据以上对话和A品牌系列空调销售的优惠办法,请你回答下列问题:
(1)求A品牌系列空调平均每次降价的百分率?
(2)请你为顾客李某决策,选择哪种优惠更合算,并说明为什么?
1)设A品牌系列空调平均每次降价的百分率为x,原价为a,根据增长率的一般公式即可列出方程解决问题;
(2)若顾客李某现在要买的A品牌系列空调的某一型号的价格为每台x元,然后分别用x表示两种方法的函数关系式,接着分情况讨论,不同情况的方法收费,比较大小即可得到结论.
解答:解:(1)设A品牌系列空调平均每次降价的百分率为x,原价为a,
根据题意,得a(1-x)2=a(1-19%),
解得x1=1.9(不合题意,舍去),x2=0.1=10%.
(2)若顾客李某现在要买的A品牌系列空调的某一型号的价格为每台x元,
按照优惠方案一每台需支付y1元,按照优惠方案二每台需支付y2元,
则y1=0.95x+90,y2=0.98x,
当y1>y2时,x<3000(元),此时应选方案二;
当y1=y2时,x=3000(元),此时选两种方案都一样;
当y1<y2时,x>3000(元),此时应选方案一.
答:(1)A品牌系列空调平均每次降价的百分率为10%;
(2)当A品牌系列空调的某一型号的价格为每台<3000元时,应选方案二;
当A品牌系列空调的某一型号的价格为每台3000元时,两种方案都可以选;
当A品牌系列空调的某一型号的价格为每台>3000元时,应选方案一.
23、某商店把进价为8元的商品按每件10元售出,每天可销售200件,现采用提高售价,减少进货量的办法增加利润,已知这种商品每涨价0.5元,其每天销售量就减少10件,若经营的这种商品要达到每天获利640元,售价应定为多少?
设定价为x元,则有(x-进价)(每天售出的数量- x-100.5×10)=每天利润,解方程求解即可.
解答:解:设定价为x元,根据题意列方程得
(x-8)(200- x-100.5×10)=640,
解得x1=12,x2=16.
∵采用提高售价,减少进货量的办法增加利润,
故应将每件售价定为16元时,才能使每天利润为640元.
点评:本题考查的是一元二次方程的应用.读懂题意,找到等量关系“经营的这种商品要达到每天获利640元”准确的列出方程是解题的关键.
24、已知a、b、c满足 |a-8|+b-5+(c-18)2=0.
(1)求a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,请求出三角形的周长,若不能,请说明理由.
1)由于有限个非负数的和为零,那么每一个加数也必为零,即若a1,a2,…,an为非负数,且a1+a2+…+an=0,则必有a1=a2=…=an=0,由此即可求出a、b、c的值;
(2)根据三角形的三边关系即可判定.
解答:解:(1)由题意得:a- 8=0;b-5=0;c- 18=0,
解之得:a= 8=2 2,b=5,c= 18=3 2;
(2)根据三角形的三边关系可知,a、b、c能构成三角形.
此时三角形的周长为a+b+c=2 2+5+3 2=5+5 2.
点评:本题考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.
25、是否存在这样的非负整数m,使关于x的一元二次方程m2x2-(2m-1)x+1=0有两个实数根?若存在,请求出m的值;若不存在,请说明理由.
根据题意,要使m2x2-(2m-1)x+1=0有两个实数根,必有△=[-(2m-1)]2-4m2≥0;解出m的值,并判断其解集中是否存在符合题意的非负整数,即可得出答案.
解答:解:不存在
由题意可得:m2≠0;
故m≠0,
又△=[-(2m-1)]2-4m2≥0,
解得:m≤ 14;
而要求m为非负整数,
故这样的m不存在.
点评:总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
23、观察下列等式:
① 12+1=2-1(2+1)(2-1)=-1+2;
② 13+2=3-2(3+2)(3-2)=-2+3;
③ 14+3=4-3(4+3)(4-3)=-3+4;…
从计算结果中寻找规律,并利用这一规律计算: (12+1+13+2+14+3+…+12002+2001)(2002+1).
解:∵ 12+1=2-1(2+1)(2-1)=-1+2,
13+2=3-2(3+2)(3-2)=-2+3,
14+3=4-3(4+3)(4-3)=-3+4,…
∴ (12+1+13+2+14+3+…+12002+2001)(2002+1)
=[(-1+ 2)+(- 2+ 3)+(- 3+ 4)+…+(- 2001+ 2002)]( 2002+1)
=(-1+ 2- 2+ 3- 3+ 4+…- 2001+ 2002)( 2002+1)
=(-1 +2002)( 2002+1)
= (2002)2-12
=2002-1
=2001.
24、某小区规划在一块长32米,宽20米的矩形场地修建三条同样宽的小路,使其中两条平行,另一条与之垂直,其余部分种草,草坪的面积为570米2,小路的宽度应是多少?
设小路的宽是x米,可表示出草坪的长和宽,根据草坪的面积为570米2,可列方程求解.
解答:解:设小路的宽是x米,
(20-x)(32-2x)=570
x=1或x=35(舍去).
故小路的宽为1米.
25、百货商店服装专柜在销售中发现:某品牌童装平均每天可销售20件,每件盈利40元.为迎“六一”国际儿童节,商店决定采取降价的措施,扩大销售量,增加盈利,减少库存,经市场调查发现,如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
每天的盈利=每天的销量×每件的利润.
设每件童装降价x元,根据题意分别表示销量和每件的利润,列方程求解.
解答:解:设每件童装降价x元,根据题意得
(20+2x)(40-x)=1200,
解得 x1=10,x2=20.
因为要减少库存,所以x=20.
答:每件童装应降价20元.
点评:此题考查一元二次方程的应用,主要搞清楚利润的表达式,难度不大.
23、美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加.
(1)根据图中所提供的信息,回答下列问题:2006年底的绿地面积为 公顷 ,比2005年底增加了 公顷;在2004年,2005年,2006年这三年中,绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2008年底使城区绿地总面积达到72.6公顷,试求2008年底绿地面积对2006年底的增长率.
第一问比较简单,第二问中:绿地总面积由60公顷增加到72.6公顷,设增长率为x,就可以列出方程60(1+x)=72.6,从而求出增长率x.
解答:解:(1)由图形可知填:60,4,2005.
(2)解:设增长率为x.
依题意得:60(1+x)2=72.6,
解得:x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:2008年底绿地面积对2006年底的增长率是10%.
25、阅读下列材料,然后回答问题.
在进行二次根式计算时,我们有时会碰到如 53,23,23+1一样的式子,其实我们还可以将其进一步简化: 53=5×33×3=533 ①
23=2×33×3=63 ②
23+1=2(3-1)(3+1)(3-1)=2(3-1)(3)2-12=2(3-1)2=3-1 ③
以上这种化简的步骤叫做分母有理化, 23+1还可以用以下方法化简: 23+1=3-13+1=(3)2-123+1=3-1 ④
(1)请用不同的方法化简: 27+5
参照③式方法化简过程为:
参照④式方法化简过程为:
(2)化简: 23+1+25+3+27+5+…+22n+1+2n-1.
(1)根据已知中的例子,③的方式是:分子、分母上同时乘以与分母构成平方差公式的式子,从而化简;
④的方式是:把2化成两个数的差,利用平方差公式分解,然后约分;
(2)根据(1)的结论,直接运用计算即可.
解答:解:(1):参照③式方法化简过程为:原式= 2(7-5)(7+5)(7-5)= 7- 5;
参照④式方法化简过程为:原式= 7-57+5= (7+5)(7-5)7+5= 7- 5.
(2)原式= 3-1+ 5- 3+ 7- 5+…+ 2n+1- 2n-1= 2n-1-1.
37、m为何值时,方程x2+mx-3=0与方程x2-4x-(m-1)=0有一个公共根?并求出这个公共根.
如果设这个公共根为α,那么根据两根之和的表达式,可知方程x2+mx-3=0的两根为α、-m-α;方程x2-4x-(m-1)=0的两根为α、4-α.再根据两根之积的表达式,可知α(-m-α)=-3 ①,α(4-α)=-(m-1)②.联立①②,即可求出α、m的值.
解答:解:设这个公共根为α.
则方程x2+mx-3=0的两根为α、-m-α;方程x2-4x-(m-1)=0的两根为α、4-α,
由根与系数的关系有:α(-m-α)=-3 ①,α(4-α)=-(m-1) ②.
由②得 m=1-4α+α2③,
把③代入①得:α3-3α2+α-3=0,
即(α-3)(α2+1)=0,
∴α=3.
把α=3代入③得:m=-2.
∴当m=-2时,两个方程有一个公共根,这个公共根是3.
38、关于x的方程 kx2+(k+1)x+k4=0有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使方程两个实数根的倒数和等于0?若存在,求出k的值,若不存在,说明理由.
(1)根据x的方程 kx2+(k+1)x+k4=0有两个不相等的实数根,得出△=(k+1)2-4k× k4>0,即可得出答案;
(2)当方程两个实数根的倒数和等于0,得出 1x1+1x2=0,进而得出k的值从而得出答案.
解答:解:(1)∵x的方程 kx2+(k+1)x+k4=0有两个不相等的实数根.
∴△=(k+1)2-4k× k4>0,
∴2k+1>0,
∴k>- 12,且k≠0;
(2)∵当方程两个实数根的倒数和等于0,
∴ 1x1+1x2=0,
∴ x1+x2x1x2=0,
∴x1+x2=0,
∵x1+x2=- k+1k=0,
∴k=-1,
∵k>- 12,
∴不存在实数k,使方程两个实数根的倒数和等于0.
5、2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1)在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
(2)在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(3)甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
本题中的(1)(2)可观察统计图求出答案;(3)中可设每天传染中平均一个人传染了x个人,则由最初的一个人经过一天后传染给了x个人,即此时有(1+x)个人患病,第二天这(1+x)个人每人又传染给了x个人,即新增病例x(1+x)个,此时共有患者[1+x+x(1+x)]名,进而可列出方程,求出答案.
解答:解:(1)18日新增甲型H1N1流感病例最多,增加了75人;
(2)平均每天新增加 267-45=52.6人,继续按这个平均数增加,到5月26日可达52.6×5+267=530人;
(3)设每天传染中平均一个人传染了x个人,则
1+x+x(x+1)=9,(x+1)2=9,
解得x1=2,x2=-4(舍去).
再经过5天的传染后,这个地区患甲型H1N1流感的人数为(1+2)7=2187(或1+2+6+18+54+162+486+1458=2187),
即一共将会有2187人患甲型H1N1流感.
22、下图是小芳家2009年全年月用电量的条形统计图.
根据图中提供的信息,回答下列问题:
(1)2009年小芳家月用电量最小的是
月,四个季度中用电量最大的是第
季度.
(2)今年小芳家添置了新电器,用电量明显增加.已知今年5月份的用电量比去年5月份增长50%,今年7月份的用电量比去年7月份增加三分之一,今年5月至6月用电量增长率是6月至7月用电量增长率的1.5倍,试求小芳家今年6月份的用电量是多少千瓦时?
考点:一元二次方程的应用;条形统计图.
专题:增长率问题.
分析:(1)根据条形图找到用电量最小的月份即可;算出每个季度的用电量,比较可得用电量最多的季度;
(2)今年5月份的用电量=去年5月份的用电量×(1+50%);今年7月份的用电量=去年7月份的用电量×(1+ 13),可设6月到7月用电量月增长率为未知数,等量关系为:今年5月份的用电量×(1+5月至6月用电量增长率)×(1+6月到7月用电量增长率)今年7月份的用电量,把相关数值代入计算即可.
解答:解:(1)由图中可以看出,5月份的用电量最小;
第一季度的用电量为:192+178+162=532;
第二季度的用电量为:116+80+132=328;
第三季度的用电量为:180+198+181=559;
第四季度的用电量为:129+155+178=462;
故答案为:5,三;
(2)设6月到7月用电量月增长率为x,
由题可得:80(1+50%)(1+x)(1+1.5x)=180×(1+ 13).
解得: x1=13,x2=-2(舍去).
所以今年6月份的用电量是80(1+50%)(1+1.5× 13)=180.
答:今年6月份的用电量180千瓦时.
点评:考查由条形图得到信息及一元二次方程的应用;得到今年7月份的用电量的等量关系是解决本题的关键.
23、小明用下面的方法求出方程2 x-3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
方程
换元法得新方程
解新方程
检验
求原方程的解
2x-3=0
令 x=t,
则2t-3=0
t=32
t=32>0
x=32,
所以 x=94
x+2x-3=0
x+x-2-4=0
考点:无理方程.
专题:图表型.
分析:此方程可用换元法解方程.(1)令 x=t,则原方程可化为t2+2t-3=0;
(2)令 x-2=t,则原方程可化为t2+t-2=0.
解答:解:
方程
换元法得新方程
解新方程
检验
求原方程的解
x+2x-3=0
令 x=t,则t2+2t-3=0
t1=1,t2=-3
t1=1>0,t2=-3<0(舍去)
x=1,所以x=1.
x+x-2-4=0
令 x-2=t,则t2+t-2=0
t1=1,t2=-2
t1=1>0,t2=-2<0(舍去)
x-2=1,所以x-2=1,x=3.
点评:在解无理方程时最常用的方法是换元法,一般方法是通过观察确定用来换元的式子,如本题中(1)设 x=t,需要注意的是用来换元的式子为设 x,则x=t2;(2)设 x-2=t,需要注意的是用来换元的式子为设 x-2=t,则x-2=t2.
24、阅读下列材料,并回答下列问题:
12+2=2-2(2+2)(2-2)=2-22=1-22132+23=32-23(32+23)(32-23)=32-236=22-33143+34=43-34(43+34)(43-34)=43-3412=33-44=33-12
(1)请你依照材料的方法计算 154+45
(2)利用你探索的规律计算: 12+2+132+23+143+34… 12524+2425
考点:分母有理化.
专题:规律型.
分析:仔细观察材料,其计算方法是分母有理化,一般二次根式的有理化因式是符合平方差公式的特点的式子.
解答:解:(1) 154+45=54-45(54+45)(54-45)=54-4520=44-55=12-55.
(2) 原式=1-22+22-33+33-44+ 2424-2525=1-15=45.
点评:主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.
23、用换元法解方程(x2-x)2-5(x2-x)+6=0,解答应写出文字说明,证明过程或演算步骤.
考点:换元法解一元二次方程;换元法解分式方程.
专题:计算题.
分析:把原方程中的(x2-x)代换成y,原方程可化为,y2-5y+6=0,即可得到关于y的方程,求得y值后,代入x2-x=y,再解两个关于x的一元二次方程即可.
解答:解:根据题意x2-x=y,把原方程中的x2-x换成y,
所以原方程变化为:y2-5y+6=0,
解得y=2或3,
当y=2时,x2-x=2,无解;
当y=3时,x2-x=3,
解得,x1= 1+132,x2= 1-132,
∴原方程的解为x1= 1+132,x2= 1-132.
点评:本题主要考查换元法在解一元二次方程中的应用.换元法是借助引进辅助元素,将问题进行转化的一种解题方法.这种方法在解题过程中,把某个式子看作一个整体,用一个字母去代表它,实行等量替换.这样做,常能使问题化繁为简,化难为易,形象直观.
24、提高题,解答应写出文字说明,证明过程或演算步骤.
(1)已知代数式-2x2+4x-18
①用配方法说明无论x取何值,代数式的值总是负数.
②当x为何值时,代数式有最大值,最大值是多少?
(2)阅读下面的例题
解方程x2-|x|-2=0
解:(1)当x≥0时,原方程化为x2-x-2=0,
解得:x1=2,x2=-1(不合题意,舍去).
(2)当x<0时,原方程化为x2+x-2=0,
解得:x1=-2,x2=1(不合题意,舍去).
∴原方程的根是x1=2,x2=-2.
请参照例题解方程x2-|x-1|-1=0.
(3)假日旅行社为吸引市民组团去某风景区旅游,推出了如下收费标准:
某单位组织员工去该风景区旅游,共支付给假日旅行社旅游费用27000元,请问该单位这次共有多少员工去风景区旅游?
(1)利用完全平方式来解答;
(2)利用公式法来解方程,在解答过程中,要注意对|x-1|进行分类讨论;
(3)根据题意,先确定旅游团的人数x,显然x>25,因为如果x≤25,则费用是25×1000=25000元,而实际费用是27000元,不符;所以每个人的费用应该是1000-20(x-25)=1500-20x元,根据题意列出方程(1500-20x)x=27000,解方程即可.
解答:解:(1)①-2x2+4x-18
=-2(x2-2x)-18
=-2(x-1)2-16
∵-2(x-1)2≤0,-16<0,
∴-2(x-1)2-16<0,
∴无论x取何值,代数式的值总是负数;
②由①知,原式=-2(x-1)2-16,
∴当-2(x-1)2=0,即x=1时,代数式有最大值;
当x=1时,原式=-16.
∴当x=1时,代数式有最大值,最大值是-16;
(2)①当x-1≥0,即x≥1时,原方程化为x2-x=0,
解得:x1=1,x2=0(不合题意,舍去).
②当x-1<0,即x<1时,原方程化为x2+x-2=0,
解得:x1=-2,x2=1(不合题意,舍去).
∴原方程的根是x1=1,x2=-2;
(3)设该单位这次共有x个员工去风景区旅游.则根据题意,得
显然x>25,因为如果x≤25,则费用是25×1000=25000元,而实际费用是27000元,不符;
所以每个人的费用应该是1000-20(x-25)=1500-20x元,根据题意,得
(1500-20x)x=27000,
解得x1=30,x2=45
①当x1=30,1500-20x=900>700,符合题意;
②当x2=45,1500-20x=600<700,不符合题意,舍去.
答:该单位这次共有30个员工去风景区旅游.
点评:本题考查了解一元二次方程的方法,配方法是解一元二次方程的一种简便方法,要会灵活运用.当配方法不适合方程时,即可考虑求根公式法,此法适用于任何一元二次方程.
3、阅读与解答:
在进行二次根式化简时,我们有时会碰上如 53,23,23+1一样的式子,其实我们还可以将其进一步化简: 53=5×33×3=533?(一),?23=2×33×3=63?(二),23+1=2×(3-1)(3+1)(3-1)=2(3-1)(3)2-12=3-1?(三), 23+1还可以用以下方法化简: 23+1=3-13+1=(3)2-123+1=(3+1)(3-1)3+1=3-1(四)
以上这种化简的方法叫做分母有理化.
(1)请用不同的方法化简 25+3.①参照(三)式得 25+3=
.
②参照(四)式得 25+3=
.
(2)化简: 23+1+25+3+27+5+…+22009+2007
考点:分母有理化.
专题:规律型.
分析:解答本题要认真阅读前面的分析,根据题目的要求选择正确的解题方法.
解答:解:(1)①原式= 2(5-3)(5+3)(5-3)= 2(5-3)5-3= 5-3.
②原式= (5)2-(3)25+3= (5+3)(5-3)5+3= 5-3.
故应填 5-3.
(2)原式=2 (3-1(3+1)(3-1)+5-3(5+3)(5-3)+7-5(7+5)(7-5)+
+ 2009-2007(2009+2007)(2009-2007))
= 2(3-12+5-32+7-52++2009-20072)
= 3-1+5-3+7-5++2009-2007
= 2009-1.
故应填 2009-1.
点评:主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.
24、说明:不论x取何值,代数式x2-5x+7的值总大于0.并尝试求出当x取何值时,代数式x2-5x+7的值最小?最小值是多少?
考点:二次函数的最值.

专题:计算题.
分析:把代数式x2-5x+7通过配方后即可证明总大于0,根据二次函数的性质即可求出最小值.
解答:解:原式=(x -52)2+ 34.
∵(x -52)2≥0.
∴原式>0恒成立;
当x= 52时,原式有最小值为 34.
点评:本题考查了二次函数的最值,难度一般,关键是掌握用配方法求二次函数的最值.
5、有这样一类题目:将 a±2b化简,如果你能找到两个数m、n,使m2+n2=a且 mn=b,则将 a±2b将变成m2+n2±2mn,即变成(m±n)2开方,从而使得 a±2b化简.
例如,5+ 26= 3+2+26= (3)2+(2)2+22•3=(3+2)2,
∴ 5+26=(3+2)2=3+2.
请仿照上例解下列问题:
(1) 5-26;
(2) 4+23.
考点:二次根式的性质与化简.
专题:阅读型.
分析:观察所给示例的结构特点,根据所给示例解答即可.
解答:解:5-2 6=3+2-2 6= (3-2)2,
∴ 5-26= (3-2)2= 3-2;
∵ 4+23= 3+1+23= (3+1)2,
∴ 4+23= (3+1)2= 3+1.
点评:本题是一个示例探究题.解题时不仅要注意探索得到的结论,更要注意探索的过程,培养逻辑思维能力和探究能
26、如图1,若要建一个长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
求:(1)若鸡场面积150平方米,鸡场的长和宽各为多少米?
(2)鸡场面积可能达到200平方米吗?
(3)如图2,若在鸡场内要用竹篱笆加建一道隔栏,则鸡场最大面积可达多少平方米?
考点:二次函数的应用.
分析:(1)若鸡场面积150平方米,求鸡场的长和宽,关键是用一个未知数表示出长或宽,并注意去掉门的宽度;
(2)求二次函数的最值问题,因为a<0,所以当(x- 354)2=0时函数式有最大值.
(3)此题中首先设出鸡场的面积和宽,列函数式时要注意墙宽有三条道,所以鸡场的长要用篱笆的周长减去3个宽再加上大门的宽2米,再求函数式的最大值.
解答:解:(1)设宽为x米,则:x(33-2x+2)=150,
解得:x1=10,x2= 152(不合题意舍去),
∴长为15米,宽为10米;
(2)设面积为w平方米,则:W=x(33-2x+2),
变形为:W=-2(x -354)2+ 12258,
∴鸡场面积最大值为153 18<200,即不可能达到200平方米;
(3)设此时面积为Q平方米,宽为X米则:Q=x(33-3x+2),
变形得:Q=-3(x -356)2+ 122512,
∴此时鸡场面积最大值为 122512.
点评:此题主要考查了一面靠墙矩形面积求法,以及二次函数最值问题,题目比较典型,是中考中热点问题.
已知 a+1a=-1+10,求 a2+1a2的值.
考点:二次根式的混合运算;完全平方公式.
分析:用完全平方公式可得: (a+1a)2=a2+2a• 1a+ 1a2=a2+2+ 1a2,这样可求得代数式的值.
解答:解:∵ (a+1a)2=a2+2a• 1a+ 1a2=a2+2+ 1a2
∴a2+ 1a2= (a+1a)2-2
= (-1+10)2-2
=1-2 10+10-2
=9-2 10.
点评:本题考查完全平方公式的运用,计算过程中注意二次根式的运算.
19、若 a+1+ b-1=0,求a2008+b2009的值.
考点:非负数的性质:算术平方根.
分析:首先根据算术平方根的非负性,求出a与b的值,然后代入多项式a2008+b2009中.
解答:∵ a+1+b-1=0,
∴a+1=0,b-1=0,
解得a=-1,b=1,
∴a2008+b2009=(-1)2008+12009=2.
点评:本题主要考查了算术平方根的非负性,以及指数的计算.
23、阅读理解:将下列二次三项式在实数范围内分解因式:
(1)x2-5x+6;(2)x2-2x+1;(3)4x2+8x-1.
解(1)令x2-5x+6=0,解得方程的两根为x1=2,x2=3.则x2-5x+6=(x-2)(x-3)
(2)令x2-2x+1=0,解得方程的两根为x1=x2=1,则x2-2x+1=(x-1)2;
(3)令4x2+8x-1=0,解得方程的两根为 x1=-2+52,x2=-2-52,则4x2+8x-1=4(x- -2-52)( x--2-52)=( 2x+2-5)( 2x+2+5)
参考以上解答下列问题:
在实数范围内因式分解:
①25x2+10x+1②4x2-8x+1
二次三项式2x2-3x+2在实数范围内能分解因式吗?如果能,请你分解出来;如果不能分解,请说明理由.
考点:实数范围内分解因式;因式分解-十字相乘法等.
专题:阅读型.
分析:根据范例的解答过程,先分别令各个二次三项式等于0,得到关于x的一元二次方程,再解出各一元二次方程的解,根据公式ax2+bx+c=(x-x1)(x-x2)分解即可.
解答:解:①令25x2+10x+1=0,解得方程的两根为x1=x2=- 15.则25x2+10x+1=(x+ 15)2;
②令4x2-8x+1=0,解得方程的两根为x1= 2+32,x2= 2-32.
则4x2-8x+1=(x- 2+32)(x- 2-32);
③令2x2-3x+2=0,由于△=b2-4ac<0,所以方程无实根,
所以二次三项式2x2-3x+2在实数范围内不能分解因式.
点评:本题考查十字相乘法分解因式,在实数范围内分解因式的步骤是:首先令二次三项式等于0,然后解一元二次方程,方程有解,则根据ax2+bx+c=(x-x1)(x-x2)公式分解,若方程无解,则原二次三项式不能分解因式.
24、已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:无论k取任意实数值,方程总有实数根.
(2)若等腰三角形ABC的一边a=1,另两边长b、c恰是这个方程的两个根,求△ABC的周长.
考点:根的判别式;三角形三边关系;等腰三角形的性质.
专题:分类讨论.
分析:1、把一元二次方程根的判别式转化成完全平方式的形式,得出△≥0可知方程总有实数根.
2、根据等腰三角形的性质分情况讨论求出b,c的长,并根据三角形三边关系检验,综合后求出△ABC的周长.
解答:证明:(1)∵△=b2-4ac=(k+2)2-8k=(k-2)2≥0,
∴无论k取任意实数值,方程总有实数根.
解:(2)若b=c,则k=2
∴x2-4x+4=0
∴x1=x2=2
∴△ABC的周长为5
若b≠c,则方程有一根为1
∴k=1,此时另一根为2,1、1、2不能构成三角形
综上所述,所求△ABC的周长为5
点评:考查根的判别式,等腰三角形的性质及三角形三边关系.
23、阅读理解题:一次数学兴趣小组的活动课上,师生有下面一段对话,请你阅读完后再解答下面问题:
老师:同学们,今天我们来探索如下方程的解法:(x2-x)2-8(x2-x)+12=0.
学生甲:老师,先去括号,再合并同类项,行吗?
老师:这样,原方程可整理为x4-2x3-7x2+8x+12=0,次数变成了4次,用现有的知识无法解答.同学们再观察观察,看看这个方程有什么特点?
学生乙:我发现方程中x2-x是整体出现的,最好不要去括号!
老师:很好.如果我们把x2-x看成一个整体,用y来表示,那么原方程就变成y2-8y+12=0.
全体同学:咦,这不是我们学过的一元二次方程吗?
老师:大家真会观察和思考,太棒了!显然一元二次方程y2-8y+12=0的解是y1=6,y2=2,就有x2-x=6或x2-x=2.
学生丙:对啦,再解这两个方程,可得原方程的根x1=3,x2=-2,x3=2,x4=-1,嗬,有这么多根啊.
老师:同学们,通常我们把这种方法叫做换元法.在这里,使用它最大的妙处在于降低了原方程的次数,这是一种很重要的转化方法.
全体同学:OK!换元法真神奇!
现在,请你用换元法解下列分式方程 (xx-1)2-5(xx-1)-6=0.
考点:换元法解分式方程;解一元二次方程-因式分解法.
专题:阅读型.
分析:换元法即是整体思想的考查,解题的关键是找到这个整体,此题的整体是 xx-1,设 xx-1=y,换元后整理并求得y得值,再代入 xx-1=y中求x得值.
解答:解:设y= xx-1,
则原方程可变为y2-5y-6=0,
解得y1=6,y2=-1,
∴ xx-1=6, xx-1=-1,
解得x= 12或 15,
经检验,都是原方程的根.
∴原方程的解为x= 12或 15.
点评:用换元法解分式方程时常用方法之一,它能够把一些分式方程化繁为简,化难为易,对此应注意总结能用换元法解的分式方程的特点,寻找解题技巧.
24、春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27 000元.请问该单位这次共有多少员工去天水湾风景区旅游?
考点:一元二次方程的应用.
专题:其他问题.
分析:首先根据共支付给春秋旅行社旅游费用27 000元,确定旅游的人数的范围,然后根据每人的旅游费用×人数=总费用,设该单位这次共有x名员工去天水湾风景区旅游.即可由对话框,超过25人的人数为(x-25)人,每人降低20元,共降低了20(x-25)元.实际每人收了[1000-20(x-25)]元,列出方程求解.
解答:解:设该单位这次共有x名员工去天水湾风景区旅游.
因为1000×25=25000<27000,所以员工人数一定超过25人.
可得方程[1000-20(x-25)]x=27000.
整理得x2-75x+1350=0,
解得x1=45,x2=30.
当x1=45时,1000-20(x-25)=600<700,故舍去x1;
当x2=30时,1000-20(x-25)=900>700,符合题意.
答:该单位这次共有30名员工去天水湾风景区旅游.
点评:此类题目贴近生活,有利于培养学生应用数学解决生活中实际问题的能力.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.
 爱华网
爱华网