wuyueshu youhua fangfa
无约束优化方法
unconstrained optimization method
研究寻求多元函数()=(,,…,)在整个实维空间中局部极小值点的数值方法它在非线性规划的研究中占有很重要的位置,除了本身的意义与应用外,它也是许多带约束优化方法的基础。
大多数无约束优化方法都是迭代法,每一次迭代都从某一点[740-13]移到另一个适合条件
([740-12])<([740-13]) (1)的点[740-12]为了得到[740-12],首先要确定移动的方向 s[740-13],其次要确定沿方向 s[740-13]移动的步长,于是[740-12]=[740-13]+s[740-13]。对应于s[740-13]与的不同选取,就得到不同的算法。
直接法 往往以直观或以计算实践为基础而产生,这类算法的特点是只要求计算函数值本身,因而易于使用,但是与另一些要求计算偏导数值的方法相比,又收敛得慢。所以直接法常常用于变量极少而函数比较复杂且不易计算偏导数的情形。较为常用的直接法有鲍威尔法、单纯形调优法和模式搜索法。
最陡下降法和牛顿-拉弗森方法 在要求计算偏导函数值的算法类中,一般取移动方向s[740-13]满足
[740-02], (2)这里的T表示矩阵(或向量)的转置运算,()表示()在点上的梯度,即
[740-03]。式(2)保证了在以[740-13]为始点,s[740-13]为方向的半直线
[740-04] (3)上一定有点适合()([740-13])。为了使式(2)成立,往往取
[740-05], [kg2] (4)式中是一阶的对称正定矩阵。
通常,步长的选取原则是取使[740-12]为()在半直线(3)上的最小值点。这样选取步长 的过程称为精确线性搜索或简称线性搜索。这时有
[740-06], (5)亦即点[740-12]上的梯度方向与移动方向成正交。
只要([740-13])≠0,总可以按上述方法进行迭代。在一定的假设下,能够证明([740-13])→0,于是对于凸函数(),点列{[740-13]}的任何极限点都是()的最小值点;而对于一般的非凸函数,即使不能保证{[740-13]}的极限点是局部最小值点,但因目标函数值逐次减少,往往也能得到满意的结果。
可以证明,在由[kg2][740-13]出发的所有同样长度的方向中,负梯度方向是使函数值下降最快的方向。于是取移动方向s[740-13]为负梯度方向-([740-13]),或者等价地取(4)中的为单位矩阵,并由线性搜索确定步长与下一点 [740-12]。这就是通常所谓的最陡下降法。
牛顿-拉弗森法则以 ()的二次近似[740-07][740-07-1]为基础,在二阶偏导数矩阵([740-13])为正定时,以此二次近似的最小值点为下一点,即取
[740-08],但这样得到的 [740-12] 未必适合式(1),因此又改成以[740-09][740-09-1]为移动方向,或者等价地在(4)中取为(([740-13]))(,再通过线性搜索来确定 与[740-12]。
在一些有关()的假设下,对于这两个古老的方法,都可证明([740-13])→0这两个方法各有其优缺点。最陡下降法比较简单,并且除了函数值本身外,只需要计算一阶偏导数的值;但是理论分析和计算实践都表明这个方法的收敛速度很慢。事实上,由 [740-10]及式(5)可知,{[740-13]}中的点沿着相互正交的方向交替前进,因此,即使对于二次严格凸函数
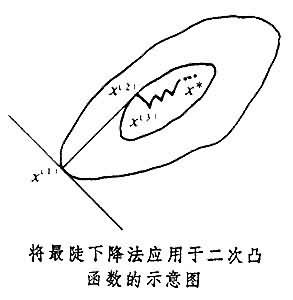
[740-11], (6)式中对称正定,只要不是数量矩阵,那么[740-13]就曲折前进,且进展很慢。当=2时如图[将最陡下降法用于二次凸函数的示意图]所示。
与此相反,牛顿-拉弗森方法收敛得快。特别对于形如(6)的二次严格凸函数,只要一次迭代,就能达到最优解,即使对于一般的函数(),[kg2]在某些假设下,也可证明{[740-13]}为二阶收敛。这个方法不仅要计算 个一阶偏导数,而且还要计算[741-01]个二阶偏导数,因此只在比较小或函数比较简单的情形才使用。
共轭梯度法与变尺度法是既有较快的收敛速度又无需计算二阶偏导函数的算法。
共轭梯度法 由于在局部最小值点的邻近,函数的性状与二次凸函数 (6)十分相似,所以对
于一个好的寻优方法,人们要求它在应用于二次凸函数时有较快的收敛速度,即使最小值点不能象牛顿-拉弗森方法那样一步达到,也应在有限步内达到。事实上,沿着空间中个两两正交的方向依次作线性搜索,一定可以达到函数1/2 (-)(-) 的最小值点。于是通过变换=(,沿着空间中个满足
[741-02] (7)的方向s(,s(,…,s依次作线性搜索,就一定能达到函数(6)的最小值点。满足式(7)的个非零方向 s(,s(,…,s称为关于矩阵[kg2]的共轭方向系。20世纪60年代R.弗莱彻和C.M.里夫斯用梯度向量构造出共轭方向系,提出了共轭梯度法。它从任意的初始点(开始,在第次迭代时取移动方向
[741-03]然后沿着半直线(3)作线性搜索得到[740-12]。在将它应用于二次凸函数(6)时,它就是一个共轭方向法,最多次迭代就能达到最小值点。共轭梯度法也适用于非二次的目标函数。在将共轭梯度法应用于非二次的目标函数时,常常采用周期性重开始的策略,也就是说,对于除余1的自然数,移动方向s[740-13]都取为负梯度方向-([740-13]),而对其他的,[kg2]s[740-13]则由(8)中第二个公式定义,采用这种策略,数值效果将有显著改进,理论上也可证明可以达到步二阶收敛,也即存在正常数使对充分大的,都有
[741-04]而若不采取周期性重开始的策略,其收敛阶仅为线性。共轭梯度法由于只需要存贮几个向量,特别适宜于解大型问题。当然,还需要采用条件予优的方法以加速收敛。
变尺度方法 也有人称为拟牛顿方法。这是近二十多年来发展起来的一类很有成效的寻优方法。理论分析和计算实践都表明这类方法的收敛速度较快,同时又无需计算二阶偏导数矩阵这类方法的共同特点是:移动方向s[740-13]由(4)定义,其中为阶对称正定方阵;可以任意选取,但通常取=;当>1时,由-1和[741-05][741-5]以及[741-06]确定,并满足如下的拟牛顿方程
[741-07] (9)步长和下一点[740-12]由线性搜索确定。
第一个变尺度法是W.D.戴维登于1959年首先提出的,而由 R.弗莱彻和 M.J.D.鲍威尔在理论上作了研究并于1963年公开发表,所以通常称为DFP方法,在这个方法中,(>1)的定义如下:
[741-08]。
由于DFP方法的成功,在其后十多年间,又提出了许多变尺度方法,这些方法只在(>1)的定义方法上有所不同。在理论上,只要[j2]、取得相同,那么在一定条件下,由不同的变尺度方法产生的点列{[740-13]}都只依赖于某一参数;但在实际计算中,由于舍入误差的关系,由不同的变尺度方法产生的点列未尽相同。最成功的变尺度法是BFGS法,它的(>1)定义为
[741-09]与DFP方法相比,BFGS方法具有较好的数值稳定性。
无论是DFP方法或者 BFGS方法,都有以下一些性质:①只要初始的矩阵正定,那么以后的各个矩阵(≥1)也都正定;②将它们应用于二次严格凸函数(6)时,由算法所确定的移动方向序列s(,s(,…,s是一组关于矩阵的共轭方向系,所以最多经过次迭代,一定能够达到二次严格凸目标函数的最小点;③理论上可以证明这两个算法在一定的条件下都是超线性收敛并且都是步二阶收敛的。
不精确线性搜索或可接受点准则 前述各法都是建立在线性搜索的基础之上的,即取[740-12]恰为()在半直线(3)上的最小值点,但在实际计算中,无法做到;虽然可以用黄金分割、二次插值等方法做到充分的近似,却极为费时。近年来,人们注意建立在不精确线性搜索的基础之上的方法。鲍威尔于1976年证明了:用适当的不精确线性搜索代替线性搜索后,BFGS算法仍是超线性收敛的。80年代,又出现了信赖域方法和基于锥模型的优化算法,已取得了良好的效果,受到了广泛的重视。
最小平方和问题 一类具有特殊形式的无约束优化问题。在这类问题中,目标函数()是一些函数的平方和,即[741-10]。这类问题在数据拟合中经常出现,方程组的求解也可转化为最小平方和的问题。由于
目标函数具有特殊的形式,所以人们设计了专门的方法,如高斯-牛顿方法、莱文贝格-马夸特方法等。
参考书目
R. Fletcher,Prcticl Methods of Optimiztion,Unconstrined Optimiztion, Vol.1, John Wiley &Sons, New York, 1979.
吴方 何旭初
以上就是网友分享的关于"无约束优化方法"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网