选择题具有题目小巧,答案简明;适应性强,解法灵活;概念性强、知识覆盖面宽的特征,它有利于考核学生的基础知识,有利于强化分析判断能力和解决实际问题的能力的培养。选择题解题的基本原则是:“充分利用选择题的特点,小题尽量不要大做” 。数学单选题的解法一般有如下几类方法:
1.直接法:从题目的已知条件出发,经过演算、推理或证明,得出与选择题的某一选项相同的结论,这种决定选择项的方法,称为直接法。
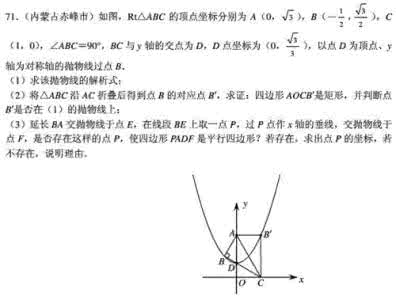
例1.如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5
C.3<OM<5 D.4<OM<5
剖析:由于动点M在弦AB上运动,当点M与点A(或B) 重合时, OM取最大值,当OM为弦心距时取最小值。
解:连接OA,过点O作OM1⊥AB于点M1。当动点与点M1重合时,OM取得最小值.此时OM1=3。当动点M与点A(或B)重合时,OM取得最大值,其最大值为OA=5。
综上,得3≤OM≤5。故应选择A。
说明:本例的解法为直接法,解选择题时虽不要求写出过程,但每一步的计算或推理仍不可大意,否则将会出现错误。
例2:若X是4和9的比例中项,则X的值为( )
A、6 B、-6 C、±6 D、36
剖析:此题考查比例中项的概念,由于4和9的比例中项为X,即X2=4×9=36,所以,X=±6都符合比例中项的定义,即 62 = 36 及(-6 )2 = 36,故4和9的比例中项应为±6,故应选择C。
2.图像法:在解答某些单项选择题时,可先根据题设作出相应的图形(或草图),然后根据图形的作法和性质,经过推理判断或必要的计算,选出正确的答案。

例3.若点(-2,y1)、(-1,y2)、(1,y3)都在反比例函数y=-的图象上,则( )
A.y1>y2>y3 B.y2>y1>y3
C.y3>y1>y2 D.y1>y3>y2
剖析:画出反比例函数y=-图象的草图,在图象上标出上述三点,便可比较y1、y2、y3的大小关系。
解:画出反比例函数y=-图象的草图.在此图象上标出点(-2,y1)、(-1,y2)、(1,y3),观察图象便知:y2>y1>y3。故应选B。
说明:本例的解法是数形结合法,与直接法相比更显得别有“洞天” 。
3. 排除法:经过推理判断,将四个备选答案中的三个迷惑答案一一排除,剩下一个答案是正确的答案,排除法也叫筛选法。
例4、若a>b,且c为实数,则下列各式中正确的是( )
A、ac>bc B、ac<bc C、ac2>bc2 D、ac2≥bc2
剖析:由于c为实数,所以c可能大于0、小于0、也可能等于0。
当=0时,显然A、B、C均不成立,故应排除A、B、C。对于D来说,当c>0,c<0,c=0时,ac2≥bc2都成立,故应选D。
例5、在下列四边形中,是轴对称图形,而不是中心对称图形的是( )
A、矩形 B、菱形 C、等腰梯形 D、一般平行四边形
剖析:由于此题要作出双重判断,因此可以先判断出轴对称图形,再排除其中不是中心对称图形,显然,一般的平行四边形不是轴对称图形,故应排除D,而在A、B、C中,A、B是中心对称图形,故也应排除A、B,那么剩下的C符合轴对称图形,而不是中心对称图形,故应选择C。
4.赋值法:有些选择题,用常规方法直接求解较困难,若根据答案所提供的信息,选择某些特殊值进行计算,或再进行判断往往比较方便。
例6在同一坐标系内,直线l1:y=(k-2)x+k和l2:y=kx的位置可能为( )
剖析:本例中一次函数的表达式中含有字母k,可用特殊值法来解.
解:令k=1,则l1:y=-x+1,l2:y=x.其图象可能是B,因此结论A、C、D同时被淘汰.故应选择B
例7. 已知一次函数y选=kx+(1-k),若k<1,则它的图象不经过第( )象限。
A、第一象限 B、第二象限
C、第三象限 D、第四象限
剖析:此题可画出函数图象的示意图,则问题便显而易见。不过由于直线斜率和与y轴交点的纵坐标为字母,比较抽象,不易画图,我们不妨采用特殊值法,对K赋予一个特殊值,则可画出示意图,问题便迎刃而解了。
不妨令k=-2,则一次函数y=KX+(1-K)变为y=-2x+3,
它示意图如图所示,不难看出它的图象不经过第三象限,故应选择C.
 爱华网
爱华网