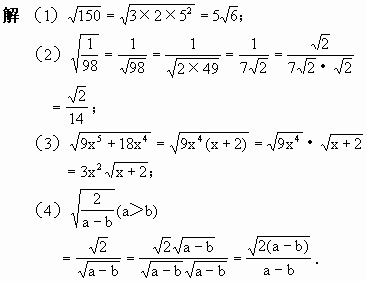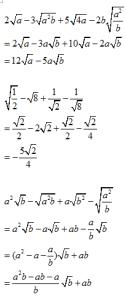人教版二次根式教案 人教版16章二次根式教案2-3

第3课时

教学目标

1. 理解最简二次根式的概念，并运用它把不是最简二次根式的化成最简二次根式．

2. 通过计算或化简的结果来提炼出最简二次根式的概念，并根据它的特点来检验最后结果是否满足最简二次根式的要求．

教学重点

最简二次根式的运用．

教学难点

会判断这个二次根式是否是最简二次根式．

教学过程

一、问题导入 教师引导学生观察上节课例题中的最后结果，比如22，32a，等，看看有什么a10

特点.

通过观察，发现这些式子中的共同点，从而总结出最简二次根式的概念.

二、新课教学

通过观察，我们可以发现这些式子有如下两个特点：

1. 被开方数不含分母；

2. 被开方数中不含能开得尽方的因数或因式．

我们把满足上述两个条件的二次根式，叫做最简二次根式．在二次根式的运算中，一般要把最后结果化为最简二次根式，并且分母中不含二次根式．

现在我们来看本章引言中的问题.

如果两个电视塔的高分别是h1km，h2km，•那么它们的传播半径的比是式子是最简二次根式吗？如果不是，把它们化成最简二次根式．

学生分组讨论，推荐3～4个人到黑板上板书．

师生总结：不是． 2Rh12Rh2．这个

2Rh1

2Rh2＝2Rh12Rh2＝h1h2＝h1h2h2h2＝h1h2. h2

通过化简，我们哭看到，这个比与地球的半径无关. 这样，只要知道h1，h2，就可以求出比值.

例 设长方形的面积为S，相邻两边长分别为a，b，已知S＝23，b＝，求a. 解：因为S＝ab，所以

a＝S232＝＝＝. b5

三、巩固练习

教材第10页练习2、3题.

四、应用拓展

观察下列各式，通过分母有理数，把不是最简二次根式的化成最简二次根式：

（1）111； （2）； （3）. 21243

解：（1）2111(21)＝＝＝2－1； 2121(2121)

（2）211(32)＝＝＝2； 3232(2)(2)

1＝4. （3）同理我们可得：

教师引导学生从上面计算结果中找出规律，并利用这一规律计算下式： （1111＋＋＋……＋）×（2002＋1）. 2132420022001

分析：由题意可知，本题所给的是一组分母有理化的式子，因此，分母有理化后就可以达到化简的目的．

解：原式

＝(2－1＋－2＋4－＋……＋2002－2001)×(2002＋1) ＝(2002－1)×(2002＋1)

＝2002－1＝2001.

五、归纳小结

最简二次根式的概念及其运用．

六、布置作业

习题16.2第7、9、13题．

爱华网本文地址 » http://www.aihuau.com/a/330451/897225087730.html