近年来,全国各省市的中考题中,考核二次函数及其相关内所占的比例较大,选择题、填空题、综合题,每个题型都有涉及。选择和填空题首要考查二次函数的意义、性质等知识点;综合题常与方程、一次函数、反比例函数、圆等知识综合在一起,有些综合题也会考核学生运用。
虽然公益课上主讲记忆方法和学习方法,但是,为了孩子考出好成绩,我也会为孩子分享一些学习资料。现在,我将初中二次函数的考点做了一些整理,分享给孩子:
考点一:二次函数的有关概念
一般的,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数。
二次函数y=ax2+bx+c(a≠0)的几种特别情势:

(1) 若b=c=0,则y=ax2;
(2) 若b=0,c≠0,则y=ax2+c;
(3) 若b≠0,c=0,则y=ax2+bx。
考点二:二次函数的图像及几种首要情势的特性
(1) 二次函数y=ax2+bx+c(a≠0)的图像是一条抛物线,当a>0时,抛物线开口 向上;当a<0时,抛物线开口>
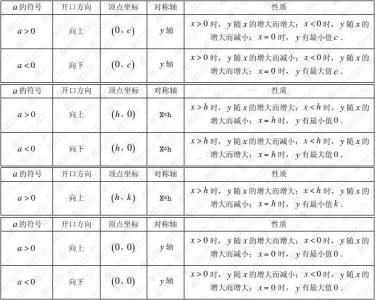
(2) 几种常见情势的抛物线的特性(对称轴、顶点坐标)
顶点式、一般式、交点式之间可以互化,如果抛物线y=ax2+bx+c(a≠0)与x轴有两个交点(x1,0),(x2,0),则可写成y=a(x-x1)(x-x2),可把y=ax2+bx+c通过配法子 化成顶点式y=a(x+ b/2a)2+ (4ac-b2)/4a。
考点三:二次函数y=ax2+bx+c(a≠0)的变更情况 (增减性)
(1) 当a>0时,在对称轴左侧(x<-b a),y随x的增大而减小;在对称轴右侧(x="">-b/2a),y随x的增大而增大。
(2) 当a<><-b a),y随x的增大而增大;在对称轴右侧(x="">-b/2a),y随x的增大而减小。
考点四:二次函数y=ax2+bx+c(a≠0)的最值
(1) 当a>0时,抛物线y=ax2+bx+c有最低点,函数有最小值,当x=-b/2a时,y最小=(4ac-b2)/4a。
(2) 当a<0时,抛物线y=ax2+bx+c有最高点,函数有最大值,当x=-b a时,y最大="">
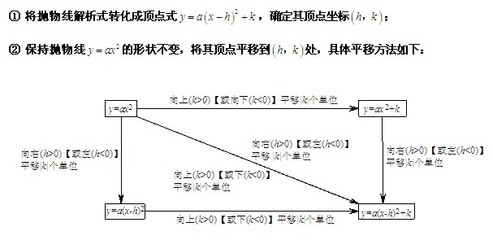
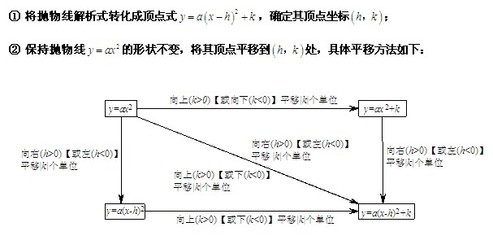
考点五:二次函数图像的平移规律
任意抛物线y=ax2+bx+c(a≠0)可以由抛物线y=ax2经过适当 的平移得到, 平移后抛物线开口 方向、开口 大小不变,即a不变;平移时“上加下减”“左加右减”。
考点六:求二次函数的解析式
用待定系数法求二次函数的解析式,要根据 给定点的特性选择适宜的法子 来求解。
(1)已知顶点坐标或对称轴或最大值时,可设顶点式y=a(x-h)2+k;
(2)已知抛物线与x轴两交点坐标或已知抛物线与x轴一交点坐标与对称轴,可通过设交点式y=a(x-x1)(x-x2)来求解;
(3)所给的三个条件是任意三点时,可设一般式y=ax2+bx+c,然后组成三元一次方程组来求解
考点七:二次函数的利用
在一些实际问题中,如物体的运动 规律问题、销售利润问题、几何图形的变更问题、存在性问题等
从标题信息中抽象出二次函数的数学模型,再用函数的规矩解决这些实际问题。
 爱华网
爱华网