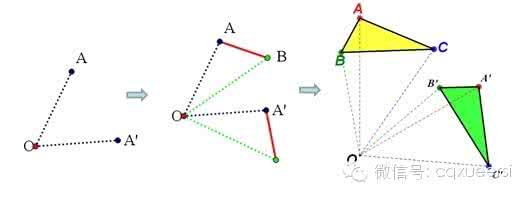
旋(xuán)转(zhuàn ):在平面内,把一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。定点叫做旋转中心,旋转的角叫做旋转角,如果图形上的点P经过旋转变为点Pˊ,那么这两个点叫做这个旋转的对应点。
旋转的重要性:初中几何三大解题思想:平移、对称、旋转。旋转算是其中最高阶的解题思想,用到压轴的几何题中,难度最大。
出题的普遍性:从选择到填空、解答的压轴,旋转普遍存在。
多数孩子现状:孩子对旋转,没有一个统一的思路和方法总结。没有能够将这一类模型总结整合成一类方便记忆和检索的方法体系。
旋转主要分类:旋转分为四大类:绕点、空翻、弦图、半角。这四类旋转的分类有似于平行四边形、矩形、菱形、正方形的分类。
一、旋转三要素
①旋转中心;
②旋转方向;
③旋转角度。
注意:三要素中只要任意改变一个,图形就会不一样。
旋转变换是由一个图形改变为另一个图形,在改变过程中,原图上所有的点都绕一个固定的点变换同一方向,转动同一个角度。(同一方向同一角度这是非常重要的,同学们在作几何旋转题一定要抓住这一点)
二、点-线-形的旋转
三、旋转的性质
①对应点到旋转中心的距离相等。(即旋转中心在对应点连线的中垂线上,这可用于“已知旋转前后图形,求旋转中心”类题型)
②对应点与旋转中心所连线段的夹角等于旋转角。(这是最重要的,根据这一性质可得出等腰三角形、等边三角形、等腰直角三角形绕着顶点旋转后,对应点所连三角形分别是等腰三角形、等边三角形、等腰直角三角形,有利于我们作出辅助线,打开思维)
③旋转前、后的图形全等。(与所求直接挂钩)
四、旋转的证明
①首先要确定旋转中心。
②弄清旋转的方向(顺时针,逆时针)和旋转的角度或度数。
③证明三角形全等。
五、图形的旋转辅助线(四大模型)
说明:
(1)旋转的目的:
(2)什么时候可以旋转:因为对应点和旋转中心连线相等,所以凡是能旋转的几何题里面,一般都会出现“共端点的等线段”,换言之,凡是出现“共端点的等线段”,一般就可以尝试利用旋转。
1、绕点
等腰三角形的旋转(遇等腰,旋顶角)
等边三角形的旋转(遇60度旋60度)
等腰直角三角形的旋转(遇90度旋90度)
实际上所有旋转都属于绕点,只是后三类较为特殊,所以单独列出。
普通绕点,也有人将其称手拉手模型或甩葱模型,记起来比较形象。
如下三组绕点题目,一目了然,灰色的这两个,确实有甩葱的意思。
2、空翻
空翻与普通绕点的区别,在于普通绕点可一眼看出旋转中心,而空翻不能。
3、弦图
弦图,也叫三垂直模型,属于极为特殊的空翻,形式上分为内弦图、外弦图,
应用上可以分为全等弦图、相似弦图(独有),其基本模型如下列三种:
4、半角
半角,属于绕点,不属于空翻,是一类极为特殊的绕点,重庆考试比较多。
凡涉及等腰直角三角形、正三角形、正四边形的图形,都可能出现半角模型。
如果孩子不知道半角、或者听过而并不会用,中考之前这个漏洞一定要补上。
特点:
过等腰△ABC(AB=AC)顶角顶点(设顶角为A),引两条射线且它们的夹角为A/2;这两条射线与过底角顶点的相关直线交于两点M、N,则BM,MN,NC之间必存在固定关系。这种关系仅与两条相关直线及顶角A相关.
解决方法:
以点A为中心,把△ACN(顺时针或逆时针)旋转角A度,至△ABN',连接MN';
结论:
1:△AMN全等于△AMN',MN=MN';
2:关注BM,MN',N'B(=NC),
若共线,则存在x+y=z型的关系;
若不共线,则△BMN'中,∠MBN'必与∠A相关,于是由勾股定理(有时需要作垂线)或直接用余弦定理可得
三者关系.
应用环境:(限于初中)
1:顶角为特殊角的等腰三角形,如顶角为30°、45°
60°、75°或它们的补角、90°;
2:正方形、菱形等也能产生等腰三角形;
3:过底角顶点的两条相关直线:底边、底角两条平分线、腰上的两高、底角的邻补角的两条角平分线,底角的邻余角另外两边等;正方形或棱形的另外两边;
4:此等腰三角形的相关弦.
以上条件可以形成数百种题目!而解决方法均可以运用此方法!
 爱华网
爱华网