第11计 耗子开门 就地打洞
●计名释义
《说唐》中有这样一个故事.唐太宗征北,困在木阳城,绝粮.军师献计,沿着鼠洞挖去,可能找到粮食.结果,真的在地下深处发现了粮仓.太宗嘉奖耗子的牙啃立功,并题诗曰:鼠郎个小本能高,日夜磨牙得宝刀,唯恐孤王难遇见,宫门凿出九条槽.
庞大的数学宝库也是众多的“数学耗子”啃穿的.你可知道,前1万个质数就是这些耗子们一个个啃出来的,七位数字对数表也是这样啃出来的.
数学解题,当你无计可施,或者一口难吞时,那就决定“啃”吧.
●典例示范
【例1】 已知f (x)=,判定其单调区间.
【分析】 用求导法研究单调性当然可行,但未必简便,直接从单调定义出发,循序渐进,也可将“单调区间”啃出来.
【解答】 设x1<x2,f (x1)-f (x2)= - .
【插语】 x1,x2都在根号底下,想法把它们啃出来.有办法,将“分子有理化”.
【续解】 [KF(S]3[]1-2x1[KF)]-[KF(S]3[]1-2x2[KF)]
=
易知=△>0.
故有原式=<0.
故f (x)= 的增区间为(-∞,+∞).
【点评】 耗子开门是一个“以小克大,以弱克强”的策略.函数的单调法即不等式的比较法.方法基础,可靠,只要有“啃”的精神,则可以透过形式上的繁杂看到思维上的清晰和简捷.
【例2】 (04·天津卷)从4名男生和2名女生中任选3人参加演讲比赛.设随机变量ξ表示所选3人中女生的人数.
(Ⅰ)求ξ的分布列; (Ⅱ)求ξ的数学期望;
(Ⅲ)求“所选3人中女生人数ξ≤1”的概率.
【思考】 本题设问简单,方向明确,无须反推倒算,只要像耗子开门,牙啃立功就是了.【解答】 (Ⅰ)6人中任选3人,其中女生可以是0个,1个或2个,P(ξ=0)=;P(ξ=1)=;P (ξ=2)=,故ξ的分布列是:
ξ
0
1
2
P
(Ⅱ)ξ的数学期望是:
Eξ=0×+1×+2×=1.
(Ⅲ)由(Ⅰ),所选3人中女生人数ξ≤1的概率是:P(ξ≤1)=P (ξ=0)+P(=1)=.
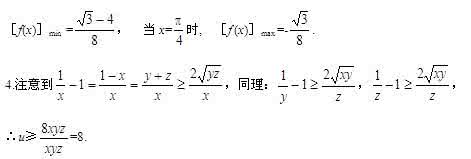
【例3】 (04·上海,20文)如图
,直线y=x与抛物线y=x2- 4交于
A、B两点,线段AB的垂直平分线与
直线y= -5交于点Q.
(1)求点Q的坐标;
(2)当P为抛物线上位于AB下方
(含点A、B)的动点时,
求△OPQ的面积的最大值.
【思考】 同例1一样,本题设问明确, 例3题图
思路并不复杂,只须按所设条件逐一完成就是,只是要严防计算失误.
【解答】 (1)由
设AB中点为M(x0,y0),则x0 =,y0=x0=1.
故有M(2,1),又AB⊥MQ,∴MQ的方程是:y-1=-2(x-2),令y=-5,得x=5,点Q的坐标为(5,-5).
(2)由(1)知|OQ|=5为定值.
设P(x,x2-2)为抛物线上上一点,由(1)知x2-4x-32≤0,得x∈[-4,8],又直线OQ的方程为:
x+y=0,点P到直线OQ的距离:
d=,显然d≠0,(否则△POQ不存在),即x≠4-4,为使△POQ面积最大只须d最大,当x=8时,dmax =6.
∴(S△POQ)max =·|OQ|·dmax=·5·6=30.
【例4】 O为锐角△ABC的外心,若S△BOC,S△COA,S△AOB成等差数列,求tanA·tanC的值.
【解答】 如图,有:S△BOC+S△AOB=2S△COA.
不妨设△ABC外接圆半径为1,令∠BOC=α=2A,
∠AOC=β=2B,∠AOB=r=2C,
则有:sinα+sinγ=sinβ,
即sin2A+sin2C=2sin2B.
2sin(A+C)cos (A-C)= 4sinBcosB. 例4题解图
∵sin(A+C)=sinB≠0,cosB= -cos(A+C).
∴cos (A-C)+2cos (A+C)=0,cosAcosC +sinAsinC+2(cosA+cosC – sinAsinC )=0.
3cosAcosC=sinAsinC,故tanAtanC=3.
【点评】 本例中的“门”不少,其中“同圆半径相等”是“门”,由此将面积关系转换成有关角的关系;以下通过圆心角与圆周角的转换,和差化积与倍角公式,诱导公式、和角公式、同角三角函数关系等依次转换,这便是一连串的“门”,逐一啃来,从而最终达到解题目的.
●对应训练
1.在棱长为4的正方体ABCD—A1B1C1D1中,
O是正方形A1B1C1D1的中心,点P在
棱CC1上,且CC1=4CP.
(Ⅰ)求直线AP与平面BCC1B1所
成的角的大小(结果用反三角函数值表示);
(Ⅱ)设O点在平面D1AP上的
射影是H,求证:D1H⊥AP;
(Ⅲ)求点P到平面ABD1的距离. 第1题图
2.证明不等式: (n∈N+).
3.设x∈,f (x)=,求f (x)的最大值与最小值.
4.若x,y,z∈R+,且x+y+z=1,求函数u=的最小值.
●参考答案
1.建立如图的空间直角坐标系,有:
A(4,0,0),P(0,4,1),B(4,4,0),B1(4,4,4),D1(0,0,4).(Ⅰ)连BP,∵AB⊥平面BCC1B1.
∴AB⊥BP,∠APB是直线AP与平面BB1C1C的夹角,∵=
∴tan∠APB=.
∴AP与平面BB1C1C所成角为arctan.
(Ⅱ)连D1B1,则O∈DB1.
∵=(4,4,0),=(-4,4,1),
∴·=-16+16+0=0.
即⊥,也就是⊥. 第1题解图
已知OH⊥面AD1P,∴AP⊥D1O(三垂线定理)
(Ⅲ)在DD1上取||=1,有Q(0,0,1),作QR⊥AD1于R,∵RQ∥AB,∴PQ∥面ABD1,∵AB⊥面AA1D1D,∴AB⊥QR,则QR⊥面ABD1,QR之长是Q到平面ABD1的距离,
∵S△ADQ =||·||=]||·||.
即:4·||= 4×3,∴||=.
已证PQ∥ABD1,∴点P到平面ABP1的距离为.
点评:虽是“综合法”证题,但也并非“巷子里赶猪,直来直去”,特别(Ⅱ),(Ⅲ)两问,本解都用到了若干转换手法.
2.只须证
右式=
=
=.
∴成立,从而1+
3.先将f (x)化为同一个角的单一三角函数,得f (x)= -sin+.
当x∈时,2x-,故f (x)为,上的减函数,当x=时,
[f(x)]min =,当x=时,[f (x)]max =-.
4.注意到,同理:,,
∴u≥=8.
 爱华网
爱华网