初中数学教案——多边形内角和
一、教材分析
七年级下册义务教育课程标准实验教科书,第七章第五节。
二、教学目标
1、知识目标:了解多边形内角和公式
2、数学思考:通过把多边形转化成三角形,体会转化思想在几何中的运用,同时让学生在体会从特殊到一般的认识问题的方法。
3、解决问题:通过探索多边形内角和公式,尝试从不同角度寻求解决问题的办法,并能有效的解决问题。
4、情感态度目标:通过猜想、推理活动感受数学活动充满着探索以及数学结论的确定性,提高学生学习热情。
三、教学的重点、难点
重点:探索多边形内角和。
难点:探索多边形内角和时,如何把多边形转变成三角形。
四、教学方法:引导发现法、讨论法
五、教具、学具
教具:多媒体课件
学具:三角板、量角器
六、教学媒体:大屏幕、实物投影
七、教学过程
(一)创设情境,设疑激思
1
老师:大家都知道三角形的内角和是180度,那么四边形的内角和你知道吗?.
活动一:探究四边形内角和。
在独立探索的基础上,学生分组交流与研讨,并汇总解决问题的方法。
方法一:用量角器量出四个角的度数,然后把四个角加起来,发现内角和是360度。
方法二:把两个三角形纸板拼在一起构成一个四边形,发现两个三角形内角和加在一起是360度。
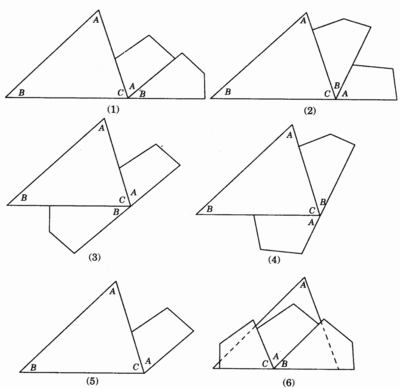
接下来,教师在方法二的基础上引导学生利用辅助线的方法,连接四边形的对角线,把一个四边形转化成两个三角形。
老师:你知道五边形的内角和吗?六边形呢?十边形呢?你是怎样的到的?
活动二:探究五边形,六边形,十边形的内角和。
学生先独立思考每个问题再分组讨论。
关注:(一)学生能否类比四边形的方式解决问题得到正确的结论。
(二)学生能否采用不同的方法。
学生分组讨论后进行交流(五边形的内角和)
方法一:把五边形分成三个三角形,三个180度是540度。
方法二:从五边形内部一点出发,把五边形分成三个三角形,然后用五个180度减去一个周角360度,结果是540度。
方法三:从五边形内部任意一点出发,把五边形分成四个三角形, 2
然后用四个180度减去一个平角180度,结果是540度。
方法四:把五边形分成一个三角形和一个四边形,然后用180度加上360度,结果是540度。
老师:你真聪明,做到了学以致用。
交流后,学生运用几何画板演示并验证得到的方法。
得到五边形的内角和后,同学们又认真地讨论起六边形、十边形的内角和。类比四边形、五边形的讨论方法最终得出,六边形内角和是720度,十边形内角和是1440度。
(二)引申思考,培养创新。
老师:通过前面的讨论,你能知道多边形内角和吗?
活动三:探究任意多边形的内角和公式。
思考:(1)多边形内角和与三角形内角和的关系?
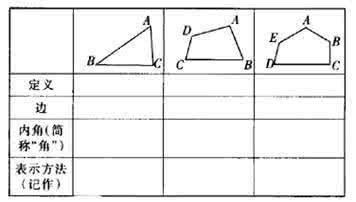
(2)多边形的边数与内角和的关系?
(3)从多边形的一个顶点引的对角线分三角形的个数与多边形的边数的关系?
学生结合思考题进行讨论,并把讨论后的结果进行交流。
发现一:四边形内角和是两个180度的和,五边形内角和是三个180度的和,六边形内角和是四个180度的和,十边形内角和是八个180度的和。
发现二:多边形的边数增加1,内角和增加180度。
发现三:一个n边形从一个顶点引得对角线分三角形的个数与边数n存在(n-2)的关系。
3
得出结论:多边形内角和公式:(n-2)*180度
(三)实际应用,优势互补
1、口答:(1)七边形内角和( )
(2)九边形内角和( )
(3)十边形内角和( )
2、抢答:(1)一个多边形内角和是1260度,它是几边形?
(2)一个多边形内角和是1440度,且每个内角都相等,则每个内角的度数是多少?
3、讨论回答:一个多边形内角和比四边形内角和多540度,并且这个多边形的各个内角都相等,这个多边形每个内角等于多少度?
(四)概括存储
学生自己归纳总结:
1、
2、
3、 多边形内角和公式 运用转化思想解决数学问题 用数形结合的思想解决问题
(五)作业练习册第92页 1、2、3
八、教学反思
1、教的转变。本节课教师的角色从知识的传授者转变为学生学习的组织者、引导者、合作者与共同研究者,在引导学生画图、测量发现结论后,利用几何画板直观地展示,激发学生自觉探究数学问题,体验发现的乐趣。
2、学的转变。学生的角色从学会转变为会学。本节课学生不是停留 4
在学会课本知识层面,而是站在研究者的角度深入其境。
3、课堂氛围的转变。整节课以“流畅、开放、合作、‘隐’导”为基本特征,教师应尽量让学生自己讨论、思考归纳总结,教学过程呈现出一种比较流畅的特征。
整节课学生与学生,学生与教师之间以“对话“、”讨论“为出发点,以互助合作为手段,以解决问题为目的,让学生在一个比较宽松的环境中自主选择获得成功的方向,判断发现的价值。 5
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网
 爱华网
爱华网