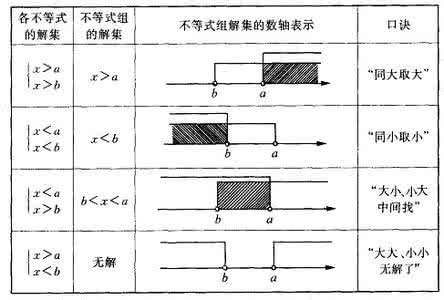
一元一次不等式组与实际生活的联系十分紧密,尤其是用它来解决方案设计问题更加方便.
一、进货方案设计型
1、某厂用甲、乙两种原料配制成某种饮料,已知这两种原料中的维生素C含量及每千克原料的价格如下表所示:
原料项目
甲种原料
乙种原料
维生素C含量 (单位/kg)
600
100
原料价格(元/kg)
8
4
现配制这种饮料10kg,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元,请根据以上条件解答下列问题:
(1)设需用xkg甲种原料,写出x所满足的不等式组;
(2)若按上述条件购买甲种原料的质量为整kg数,有几种购买方案,请写出购买方案.
分析:
(1)设需用xkg甲种原料,根据配制这种饮料10kg,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元,可列出不等式组.
(2)解出(1)的不等式组,且购买甲种原料的质量为整kg数,可得到方案.
解:(1) 600x+100(10-x)≥4200
8x+4(10-x)≤72
(2)由(1)解得 6.4≤x≤8
若按上述的条件购买甲种原料的质量为整kg数,
有两种购买方案:
方案一:甲种原料为7kg,乙种原料为3kg;
方案二:甲种原料为8kg,乙种原料为2kg.
2、某校准备组织290名学生进行野外考察活动,行李共有100件.学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.
(1)设租用甲种汽车x辆,请你帮助学校设计所有可能的租车方案;
(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案
解:(1)由租用甲种汽车x辆,则租用乙种汽车(8-x)辆,
由题意得:40x+30(8-x))≥290
10x+20(8-x)≥100
解得:5≤x≤6.
共有2种租车方案:
第一种是租用甲种汽车5辆,乙种汽车3辆;
第二种是租用甲种汽车6辆,乙种汽车2辆.
(2)第一种租车方案的费用为5×2000+3×1800=15400元;
第二种租车方案的费用为6×2000+2×1800=15600元.
∴第一种租车方案——租用甲种汽车5辆,乙种汽车3辆;更省费用.
3、某工厂要用图1所示的长方形和正方形纸板,经过组合加工成竖式,横式两种长方体形状的无盖纸盒.
(1)设加工竖式纸盒x个,横式纸盒y个,根据题意,完成下列表格:
纸盒
纸板
竖式纸盒(个)
横式纸盒(个)
X
y
正方形纸板(张)
X
2y
长方形纸板(张)
4X
3y
(2)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完.
(3)该厂在某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试问在这一天加工这两种纸盒时,a的所有可能的值.
解:(1)正方形纸板x张,长方形纸板3y张;
(2)设加工竖式纸盒x个,加工横式纸盒y个,
依题意,得
x+2y=1000 4x+3y=2000 解得:
x=200 y=400
答:加工竖式纸盒200个,加工横式纸盒400个;
(3)设加工竖式纸盒x个,加工横式纸盒y个,
依题意得:
x+2y=50 4x+3y=a ∴y=40- a/5
∵y、a为整数,
∴a为5的倍数,
∵120<a<136
∴满足条件的a为:125,130,135.
当a=125时,x=20,y=15;
当a=130时,x=22,y=14;
当a=135时,x=24,y=13据符合题意,
∴a所有可能的值是125,130,135.
4、某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个 种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个 种造型的成本是800元,搭配一个 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
解:(1)设搭配A种造型x个,则B种造型为(50-x)个,
依题意得
解得:31≤x≤33
∵x是整数,
∴x可取31,32,33
∴可设计三种搭配方案
①A种园艺造型31个B种园艺造型19个
②A种园艺造型32个B种园艺造型18个
③A种园艺造型33个B种园艺造型17个.
(2)方法一:
方案①需成本31×800+19×960=43040(元)
方案②需成本32×800+18×960=42880(元)
方案③需成本33×800+17×960=42720(元)
∴应选择方案③,成本最低,最低成本为42720元
5、某商场经销甲、乙两种商品,甲商品每件进价15元,售价20元.乙商品每件进价35元,售价45元.(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?(2)该商场为使甲、乙两种商品共100件的利润不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
分析:本题第一问中两种商品进货价恰好用去2700元,所以可以列方程直接解出.但是第二问中的利润给的是一个范围,我们只能列不等式组,找出它们的公共部分(即解集),再分析其全部的方案.
解:(1)设该商场能购进甲种商品x件,则购进乙商品(100-x)件.
由题意得:15x+35(100-x)=2700
x=40(件)
100-x=60(件)
(2)设该商场购进甲商品a件,则购进乙商品(100-a)件.
由题意得:
解这个不等式组得:48≤a≤50
∵a是正整数
所以,a的取值可以取48、49、50三种情况.
所以进货方案有三种:
方案1:购进甲商品48件,乙商品52件
方案2:购进甲商品49件,乙商品51件
方案3:购进甲商品50件,乙商品50件
例2:某水果经销商收购苹果20吨,梨12吨,现计划租用甲、乙两种货车共8辆将它们全部运出,已知一辆甲种货车可装苹果4吨和梨1吨,一辆乙种货车可装苹果和梨各2吨.
(1)经销商如何安排甲、乙两种货可一次性地将水果全部运出,有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则经销商选择哪种方案才能使运输费用最少?最少是多少?
分析:本题中可根据这两种车运输苹果、梨的能力大于或等于货物的重量,列出两个不等式,再找它们的公共部分即可.
解:(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆.
由题意得:
解这个不等式组得:2≤x≤4
∵x是正整数
∴x可取的值是2,3,4
因此甲、乙两种货车的方案有三种即:
甲种货车(辆)
乙种货车(辆)
方案一
2
6
方案二
3
5
方案三
4
4
(2)方案一所需运费:300×2+240×6=2040元
方案二所需运费:300×3+240×5=2100元
方案三所需运费:300×4+240×4=2160元
所以经销商选择方案一运输费用最少,最少费用是2040元.
例3 某建筑公司急用普通水泥230吨 刚材168吨 现有A B两种型号货车共40辆可供使用 每辆A型车最多可装普通水泥6吨和钢材4吨,运费190元;每辆B型车最多可装普通水泥5吨和钢材5吨,运费200元。
(1)要安排A、B两种型号的货车来运输,有几种方案?请你帮该公司设计。
(2)那种运输方案的运费最省钱?为什么?
解:(1)设A型货车x辆,则B型货车40-x辆,
根据题意得
6x+5(40-x)≥230
4x+5(40-x)≥168
解得30≤x≤32
∴有三种方案:
①A30辆,B10辆;
②A31辆,B9辆;
③A32辆,B8辆;
(2)因为A型车便宜,所以用A型车越多越省钱。
所以方案①费用最省钱,
此时费用是30×190+10×200=7700(元)
练习、(2007南充)某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
类 别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
计划购进电视机和洗衣机共100台,商店最多可筹集资金161 800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
二、搭配方案设计型
例4、.
三、租赁方案设计型:
例5、(2007四川绵阳)绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
练习 某汽车租凭公司要购买轿车和面包车共10辆。其中轿车至少要购买3辆。轿车每辆7万元,面包车每辆4万元。公司可投入的购车款不超过55万元。
(1)符合要求的购车方案有几种?请说明理由。
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每月都可以出租,要使这10辆车的月租金不低于1500元,那么应选择以上哪种购买方案?
分析:设要购买轿车x辆,则要购买面包车(10-x)辆,题中要求“轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元”列出不等式,然后解出x的取值范围,最后根据x的值列出不同方案.
解:(1)设要购买轿车x辆,则要购买面包车(10-x)辆,
由题意得7x+4(10-x)≤55
解得x≤5.
又因为x≥3,
∴3≤x≤5.
∵x为整数
∴x=3,4,5
因此有三种购买方案:
①购买轿车3辆,面包车7辆;
②购买轿车4辆,面包车6辆;
③购买轿车5辆,面包车5辆.
(2)方案一的日租金为:3×200+7×110=1370(元)
方案二的日租金为:4×200+6×110=1460(元)
方案三的日租金为:5×200+5×110=1550(元)
答:为保证日租金不低于1500元,应选择方案三购买轿车5辆,面包车5辆.
三、购物方案设计型:
例6、(2007广东课改)某博物馆的门票每张10元,一次购买30张到99张门票按8折优惠,一次购买100张以上(含100张)门票按7折优惠.甲班有56名学生,乙班有54名学生.
(1)若两班学生一起前往该博物馆参观,请问购买门票最少共需花费多少元?
(2)当两班实际前往该博物馆参观的总人数多于30人且不足100人时,至少要有多少人,才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜?
例7
例8、(2007福建厦门课改)小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为69千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时爸爸的一端仍然着地.后来小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地.小宝的体重可能是( ),写出解题过程。
 爱华网
爱华网