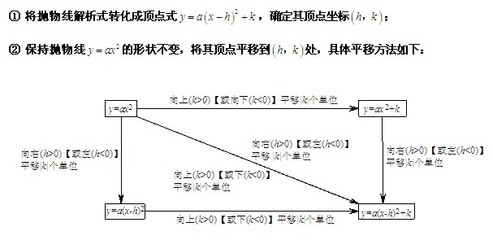
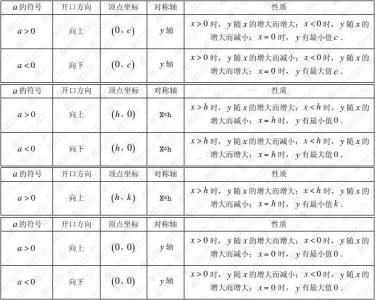
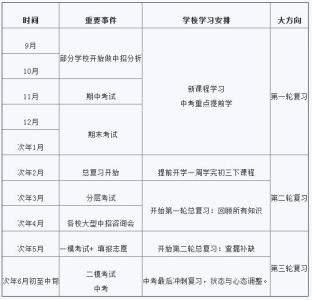
函数复习(二)
5. 函数解析式的求法
(1)换元法
[例1] 已知,求
解法1:(直接换元)
令
∴
解法2:(凑式换元法)
(2)消去法
[例2] 设满足关系式,求
解:由①用代换得
② 由①和②联立消去
得 由
从而
[例3] 已知①,,求
解:用代换得,②
由①和②联立得
[例4] 已知且,求
解:由① 用代换①中得
② 由①、②联立得
(3)待定系数法
[例5] 已知,且是一次函数,求。
解:设一次函数,则
与比较函数,得
所以
(4)赋值法
[例6] 已知,且对任何实数,有等式成立,求的解析式。
解:令作代换令得
(5)递推法
[例7] 函数满足且,求的解析式。
解:由
……
把以上个关系式相加
当时,
当时,
当时,
又法:(只考虑且时)
设
令是常数列
6. 值域的求法
(1)判别式法
[例1] 求函数的值域。
解:
① 时,
② 时,
[例2] 求函数的值域(不能用判别式,可约分式)
解:
∴ ∴
[例3] 求函数的值域。
解:
(1)当时,
(2)当时,原式即
∴
∵ 时,
∴ 解得或 ∴
(2)反函数法
[例4] 求的值域()
解: 由
∴
由 ∴(1)的解是或
(2)的解或,故或
值域
(3)配方法
[例5] 求函数,的值域。
解:,得对称轴方程
根据对称轴分类
① 时,递减值域
② 当时,对称轴在之内,值域
③ 当时,对称轴在之内,值域
④ 当时,对称轴在[0,1]之右,在[0,1]上递增
值域
(4)性质法
[例6] 求函数的值域
解:定义域R且=0
所以为奇函数
当时,单增,,因奇函数图象关于坐标原点对称,所以该函数值域为R
[例7] 求函数的值域
解:定义域R,偶函数,周期
当时,
(5)最值法
[例8] 求函数,的值域
解:
(1)时,
(2)时,=4
当且仅当即时取等号
故值域
另法利用导数
令或
(6)换元转化法
[例9] 求函数()的值域
解:令,则
(1)时,
(2)时,
[例10] 求的值域
解:令,则
由 ∴ 值域
(7)导数法
[例11] 求函数的值域
解:由
令,
又令
由或
+
0
-
0
+
↑
极大值
↓
极小值
↑
所以在()上的极大值点为,极小值点,所以在[]上,有极小值,,又由,=,所以在上的最小值点为,最大值点为,因此当即,时,取最小值,当,即,时,取极大值。
1
-
0
+
4
↓
极小值
↑
∴
【模拟试题】
1. 已知,求并解方程。
2. 设对一切实数,,求定义于区间上的函数
3. 求的值域。
4. 求函数的值域。
5. 求的值域。
6. 求函数的定义域和值域。
7. 已知函数定义域为R,值域为[0,2],求的值。
8. 已知,,且(且)
(1)确定的值;(2)求的最小值及相应的值。
【试题答案】
1. 解:
∴
由
由,由
∴ 的解是
2. 解:令,则得①
以代换式中,则有②
由①和②联立得
∴ ,
3. 解:
① 时,
② 时,
∴ 值域
4. 解:∵ 函数的定义域为
∴ 可设, ∴
∴ 原函数化为
当时,函数有最大值为2
当时,函数的最小值为
∴ 函数的值域为
5. 解:∵ ∴ ,
∴ 原函数化为
当,即,
当,即,
6. 解:由得又定义域为非空数集,则,故定义域为()
令,则对称轴为
① 当 即时,
故值域为
② 当 即时,无最大值和最小值,利用单调性,有,而,
故
故值域
7.
解:令,则,即,由,得
问题转化为有理分式函数,
值域为时,求系数的值
由
由即
该不等式解集即的值域[1,9]
即
另法由
8. 解:
(1)由已知
由,则,则上式,即
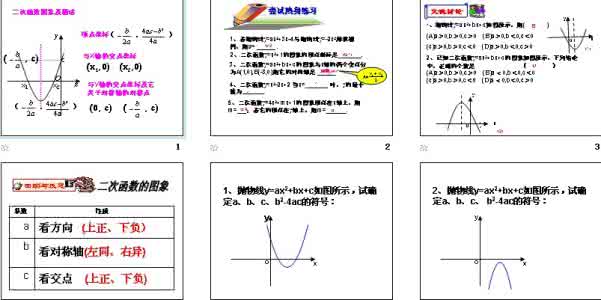
,故
(2)由,则
当且仅当即时,等号成立
此时,由 即时,取最小值。
 爱华网
爱华网