抛物线部分
【典型例题】
[例1] 如图所示,F为抛物线的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,的最小值为8。
(1)求抛物线的方程;
(2)若 O为坐标原点,问是否存在点M,使过点M的动直线与抛物线交于B、C两点。且,证明你的结论。
解:(1)由抛物线性质可知
故抛物线方程为
(2)若斜率存在,设过M的直线方程为,显然,,直线交抛物线于B、C
由
由
故
动直线方程为 即
[例2] 已知抛物线的准线与轴交于M点,过M作直线与抛物线交于A、B两点,若AB的垂直平分线与轴交于E()。
(1)求的取值范围;
(2)能否是正三角形?若能,求的值;若不能,请说明理由。
解:(1)由题意得直线:,代入,得
由,则,且
设方程两根分别为A、B两点的横坐标,则其中点坐标为
则AB的垂直平分线方程为
令,得
(2)若为正三角形,则点E到AB的距离为的倍
由()
,得
[例3] 已知抛物线C:,点A(),如果抛物线C上到点A距离最近的是抛物线C的顶点,那么的取值范围是( )
A. B. C. D.
解法一:从方程角度看命题的等价转化
方程组只有一解方程(3)
在上只有一个解
由(3)有两个解,故
解法二:从函数角度看命题的等价转化
函数(当时,有最小值)
函数(在定义域的左端点取最小值)
这样只须令二次函数的对称轴位于原点的左侧,即
解法三:从不等式角度看命题的转化
关于x、y的不等式(4)(对一切满足的实数成立,且时,等号成立)关于的不等式(5)(在上成立,且时等号成立)
由于(5)的解集是“两根之外”,因此应在大根之外,故另一根
[例4] 已知抛物线过动点M()且斜率为1的直线与抛物线交于不同的两点A、B,。
(1)求的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求面积的最大值。
解:(1)将代入,得
设直线与抛物线的两个不同的交点坐标为A(),B()
则,又
所以
因为,,所以
解得
(2)设AB的垂直平分线交AB于点Q,令坐标,则由中点坐标公式
得,
所以
又为等腰,故
因此
最大面积为
[例5] 如图,直线和相交于M,,点,以A、B为端点的曲线段C上的任一点到的距离与到点N的距离相等,若为锐角三角形,,,且,建立适当的坐标系,求曲线段C的方程。
解法一:依题意知,曲线段C是以N为焦点,以为准线的抛物线的一段,其中A、B分别为曲线C的端点,以为x轴,MN的垂直平分线为y轴建立直角坐标系,设曲线C的方程为()
其中,且M(),N()
由,,得①
②
由①、②得:,将之代入①得:或
由三角形AMN是锐角三角形知,所以,,
又由点B在曲线段C上,得:
则曲线段C的方程为:
解法二:建系,并确定C是抛物线的一段,作,,垂足分别为E、D、F,则
由为锐角三角形,故
即
故,曲线段C的方程为:()
注:此法根据抛物线定义确定曲线段方程的形式,根据图形应用条件直接确定参数。
[例6] 在y轴的负半轴上任取一点A(0,m),过点A作抛物线()的切线,切点C,交轴于点B,F为抛物线的焦点。
(1)证明:;
(2)延长CF交抛物线于另一点D,连接AD,则能否为钝角,若是钝角,求出m的取值范围,若不是,加以证明。
解:(1)抛物线的焦点为F()
设切点C(),则切线AC的方程为
令,得 即B()
令得,,即A(0,),由,则
故,
故 即
(2)设CD方程为,由
设,则,
由(1)知,
又
则
若为钝角,则
由点C、A、D不共线,则
只需即
故
由,故
所以能为钝角,此时m的取值范围为
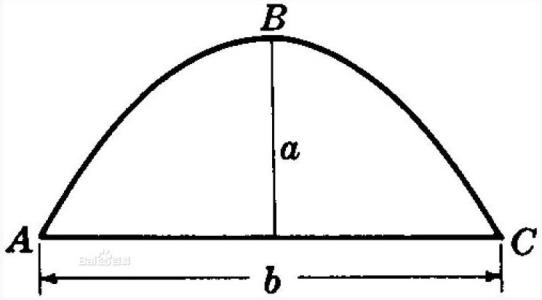
[例7] 设是一常数,如图,过点Q(2p,0)的直线与抛物线交于相并两点A、B,以线段AB为直径作⊙H(H为圆心),试证抛物线顶点O在⊙H上,并求当⊙H的面积最小时,直线AB的方程。
解法一:设
由
,
从而
则,则
故O点必在⊙H上
又H()是AB的中点,则
故,从而时,⊙H面积最小,此时
解法二:由分别消去,得
得A、B所在圆方程:
显然原点O在上面圆上,下同解法一。
[例8] 设正方形ABCD的外接圆方程为(),C、D点所在直线的斜率为。
(1)求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率;
(2)若在x轴上方的A、B两点在一条以原点为顶点以x轴对称轴的抛物线上,求此抛物线的方程及直线的方程。
解:(1)由
由,,MA、MB的斜率满足
(2)设MB、MA的倾斜角分别为,则
,
再设,则
设抛物线方程为,由于A、B两点在抛物线上,则
,
抛物线方程为,又A点坐标为(1,1),且A点关于M(3,0)的对称点C的坐标是(),直线的方程为
即
【模拟试题】
1. 过(0,1)作直线,使它与抛物线仅有一个公共点,这样的直线有( )
A. 1条 B. 2条 C. 3条 D. 4条
2. 直线与抛物线有且仅有一个公共点是直线与抛物线相切的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 不充分不必要条件
3. 在抛物线中,以()为中点的弦的方程为( )
A. B.
C. D.
4. 过抛物线的焦点F作弦,则弦的中点的轨迹方程是 。
5. 若动点P(x,y)在抛物线上移动,则P与点()的连线的中点的轨迹方程是 。
6. 过抛物线的顶点,任作两条垂直的弦OA、OB。
(1)求证:直线AB恒过一定点;
(2)求AB中点M的轨迹方程。
7. 已知⊙M:,⊙N:,动圆P与⊙M、⊙N均外切。
(1)求动圆圆心P的轨迹C的方程;
(2)延长PN与曲线C交于另一点Q,求的最小值;
(3)是否存在直线:,使得PQ的中点R在直线上的射影S满足PS⊥QS?若存在,求出的取值范围;若不存在,请说明理由。
【试题答案】
1. C 2. B 3. C 4. 5.
6. 解:(1)设,由,则直线AB的斜率为
,故AB方程为
整理得(*)
由,即
即,故(*)即=0
令,则,故AB恒过定点(0,)
(2)设AB中点M(x,y),AB斜率
由,(由AB恒过定点())
则
化简得点M的轨迹方程为
7. 解:(1)设动圆P的半径为,依题意,
两式相减得,故点P的轨迹为以M,N为焦点,焦距4,实轴长为2的双曲线右支,故C的方程:
(2)当PQ斜率不存在时,易求得
当PQ斜率存在时,设,代入双曲线方程并整理得
PQ与双曲线右支交于两点的充要条件是
得
由N为焦点,则PQ为双曲线的焦点弦,故
(由)故最小值为6
(3)直线存在时,PS⊥QS,为,则点R到的距离()
故
又
故 而,故,则
故当时,这样的直线存在,当时,这样的直线不存在
注:(3)中若,则
由
① 当时,
② 当时,
故当或时,这样的直线存在
当时,这样的直线不存在。
 爱华网
爱华网