相关解答一:如何用spss生成决策树,我生成的决策树只有一个节点,是我的数据有问题吗 10分
你的样本量多半太少了,做决策树至少要1000个样品,上万都是正常的事情
并不是所有的数据都适合决策树分析的,数据没有问题,而是你对方法的选择有问题
相关解答二:决策树的父节点和子节点哪个熵更大
一、最佳拆分
如何将纯度增加进行量化呢?用于评价拆分分类目标变量的纯度变量包括:
基尼(Gini)CART
熵(信息增益)ID3
信息增益比率 C5
卡方检验 CHAID
1、基尼
以意大利统计学家和经济学家Corrado Gini的名字命名的拆分标准,它也被生物学家和生态学家用于总体多样性研究,这种方法用于计算从相同的总体中随机选择的两项处于同一类中的概率,对于一个纯的总体,此概率为1
2、熵和信息增益
对于某个指定决策树结点,熵是该结点所代表的全部类中,每个特定类的记录的比例乘以该比例以2为底的对数后的总和,一个拆分的熵就是该拆分产生的所有结点的熵按照每个结点的记录所占比例的加权和。
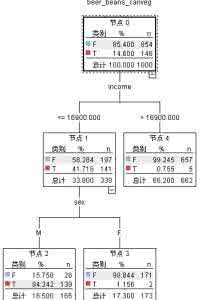
例子:两课决策树,决策树1根节点包括10个正类,10个负类(总共20个样本),左叶节点9个正类,1个负类。右叶结点9个负类,1个正类。决策树2根结点包括10个正类,10个负类,左叶结点6个正类,右叶结点4个正类,10个负类。通过GINI和信息增益判断两棵树的优劣。
GINI:第一棵树每个叶节点的GINI得分是0.1^2+0.9^2=0.820,因为子节点的大小相同,这也是该拆分的得分
第2棵树左节点=1,右结点(4/14)^2+(10/14)^2=0.592,这一拆分的基尼得分是(6/20)*1+(14/20)*0.592=0.714
第一棵树的基尼得分比第二棵的大(0.82>0.592)。
相关解答三:用SPSS 生成决策树时只有一个节点,什么原因
数据太纯了,spss会进行剪枝,每个叶子节点不会是百分之百。
你的样本量多半太少了,做决策树至少要1000个样品,上万都是正常的事情
并不是所有的数据都适合决策树分析的,数据没有问题,而是你对方法的选择有问题
相关解答四:r语言 为什么决策树只有根节点
自变量量的筛选是根据其卡方显著性程度不断自动生成父节点和子节点,卡方显著性越高,越先成为预测根结点的变量(建模需要的变量),程序自动归并预测变量的不同类
相关解答五:决策树算法是否可能左右子树存在相同的节点 10分
Void traveltree(Bitnode*root,Bit Bitnode1*root1)
{int k=0 ,j =0,k1=0,j1=0;
if(root ! =null)
{prev(root->lch)k++;
prev(root->rch)j++;
}
if(root 1! =null)
{prev(root1->lch)k1++;
prev(root1->rch)j1++;}
If(k==k1&&j==j1)
{printf(“两树相似”);
Else
{printf(“两树不相似”);
}
}
相关解答六:请问spss做决策树怎么只有根节点?结果中没有自变量啊?
很正常的
决策树不是你乱操作就可以的
对数据有严格的要求,样本量一般要大
然后数据要符合决策树的要求才行
我替别人做这类的数据分析蛮多的
相关解答七:决策树软件实现的时候CP中的rel为什么比节点数少一个啊
library(rpart);
## rpart.control对树进行一些设置
## xval是10折交叉验证
## minsplit是最小分支节点数,这里指大于等于20,那么该节点会继续分划下去,否则停止
## minbucket:叶子节点最小样本数
## maxdepth:树的深度
## cp全称为complexity parameter,指某个点的复杂度,对每一步拆分,模型的拟合优度必须提高的程度
ct
## kyphosis是rpart这个包自带的数据集
## na.action:缺失数据的处理办法,默认为删除因变量缺失的观测而保留自变量缺失的观测。
## method:树的末端数据类型选择相应的变量分割方法:
## 连续性method=“anova”,离散型method=“class”,计数型method=“poisson”,生存分析型method=“exp”
## parms用来设置三个参数:先验概率、损失矩阵、分类纯度的度量方法(gini和information)
## cost我觉得是损失矩阵,在剪枝的时候,叶子节点的加权误差与父节点的误差进行比较,考虑损失矩阵的时候,从将“减少-误差”调整为“减少-损失”
fit
data=kyphosis, method="class",control=ct,
parms = list(prior = c(0.65,0.35), split = "information"));
## 第一种
par(mfrow=c(1,3));
plot(fit);
text(fit,use.n=T,all=T,cex=0.9);
## 第二种,这种会更漂亮一些
library(rpart.plot);
rpart.plot(fit, branch=1, branch.type=2, type=1, extra=102,
shadow.col="gray", box.col="green",
border.col="blue", split.col="red",
split.cex=1.2, main="Kyphosis决策树");
## rpart包提供了复杂度损失修剪的修剪方法,printcp会告诉分裂到每一层,cp是多少,平均相对误差是多少
## 交叉验证的估计误差(“xerror”列),以及标准误差(“xstd”列),平均相对误差=xerror±xstd
printcp(fit);
## 通过上面的分析来确定cp的值
## 我们可以用下面的办法选择具有最小xerror的cp的办法:
## prune(fit, cp= fit$cptable[which.min(fit$cptable[,"xerror"]),"CP"])
fit2 >
相关解答八:什么是决策树
决策树一般都是自上而下的来生成的。每个决策或事件(即自然状态)都可能引出两个或多个事件,导致不同的结果,把这种决策分支画成图形很像一棵树的枝干,故称决策树。
参考资料:baike.baidu.com/view/589872.html?wtp=tt
相关解答九:如何画决策树
基本定义
决策树算法是一种逼近离散函数值的方法。
编辑本段算法优点
决策树算法的优点如下: (1)分类精度高; (2)成的模式简单; (3)对噪声数据有很好的健壮性。 因而是目前应用最为广泛的归纳推理算法之一,在数据挖掘中受到研究者的广泛关注。
编辑本段基本原理
决策树方法最早产生于上世纪60年代,到70年代末。由J Ross Quinlan提出了ID3算法,此算法的目的在于减少树的深度。但是忽略了叶子数目的研究。C4.5算法在ID3算法的基础上进行了改进,对于预测变量的缺值处理、剪枝技术、派生规则等方面作了较大改进,既适合于分类问题,又适合于回归问题。
编辑本段构造方法
决策树构造的输入是一组带有类别标记的例子,构造的结果是一棵二叉树或多叉树。二叉树的内部节点(非叶子节点)一般表示为一个逻辑判断,如形式为a=aj的逻辑判断,其中a是属性,aj是该属性的所有取值:树的边是逻辑判断的分支结果。多叉树(ID3)的内部结点是属性,边是该属性的所有取值,有几个属性值就有几条边。树的叶子节点都是类别标记。 由于数据表示不当、有噪声或者由于决策树生成时产生重复的子树等原因,都会造成产生的决策树过大。因此,简化决策树是一个不可缺少的环节。寻找一棵最优决策树,主要应解决以下3个最优化问题:①生成最少数目的叶子节点;②生成的每个叶子节点的深度最小;③生成的决策树叶子节点最少且每个叶子节点的深度最小。
相关解答十:决策树怎么画
建议你找一本管理信息系统的书看!画法户是一句两句话可以描述清楚的!自己学习一下!效果好一些!我也在学习中…
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网
 爱华网
爱华网