命题和充要条件
二. 知识讲解:
本考点内容在高考中主要考查基本概念和基本原理,不会单独命题,但会与其它知识结合,解逻辑问题的关键是熟练地掌握基本概念和基本方法。
1. 命题:所谓命题,是指可以判断真假的语句,命题分为真命题和假命题两种。
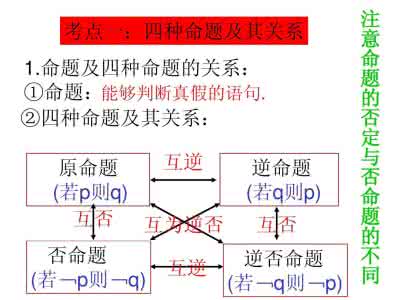
2. 命题有四种形式,即原命题、逆命题、否命题、逆否命题,其中原命题与逆否命题同真同假,逆命题和否命题同真同假,即逆否关系是等价关系。
3. 判断充要条件问题时,要注意以下几点:
(1)明确命题中的条件是什么,结论是什么;
(2)若,,则是的充分不必要条件,也称是的必要不充分条件;若,则称是的充要条件,若,,则称是的既不充分也不必要条件。
4. 要知道数学用语,如“当且仅当”,“有且仅有”是指充要条件的。
【典型例题】
[例1] 已知命题:方程有两个不相等的负实根,:方程
无实根,如果或为真,且为假,求实数的取值范围。
解:由则,即:
由,则,即:
而或为真,且为假等价于和中有且仅有一个为真,另一个为假
(1)当真假时,有则
(2)当假真时,有,则
综上,实数的取值范围是或
[例2] 设集合,,
,则点P(2,3)的充要条件是( )
A. B.
C. D.
解:由,则P(2,3)等价于
即故应选A
[例3] 一元二次方程()有一个正根和一个负根的充分不必要条件是( )
A. B. C. D.
解:设()的两根为,则方程有一个正根和一个负根,等价于即,而A是充要条件,B、D均为既不充分也不必要条件,只有C是充分不必要条件。
[例4](1)若四点不共面,则这四点中任何三点都不共线;(2)若两条直线没有公共点,则这两条直线是异面直线,以上命题中,逆命题为真命题的是( )。
解:
(1)的逆命题为:若四点中任何三点都不共线,则这四点不共面,显然为假命题。
(2)的逆命题为:若两条直线是异面直线,则这两条直线没有公共点,根据异面直线的概念可知其为真命题,所以应填(2)。
该题也可利用逆否关系的等价性进行分析。
(1)的逆命题与否命题等价,否命题为:若四点不共面,则这四点中存在三点共线,它是假命题。
(2)的否命题为:若两条直线有公共点,则这两条直线不是异面直线,它是真命题,故应填(2)。
【模拟试题】
一. 选择题:
1. 设全集为U,A、B为U的子集,则下列命题中与等价的有( )
① ,② ,③ ,④
A. 1个 B. 2个 C. 3个 D. 4个
2. 已知:,:的两根介于和4之间,则是的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 如果是B的充分而不必要条件,那么A是B的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 已知,,其中为正实数,则,,同时成立是成立的是( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分也不必要条件
二. 填空题:
5. “对任意实数,不等式()成立,则,”的逆命题,否命题和逆否命题中,真命题共 个。
6. 下列四个命题:
① “”是“,或”的充分不必要条件
② “”是“”的必要不充分条件
③ “”是“有实根”的充分不必要条件
④ “”是“”的充要条件
⑤ “若,则”的逆否命题是“若”,则,其中真命题的序号是 。
【试题答案】
一. 选择题:
1. D 2. A 3. B 4. C
二.
5. 3
6. ①②③
 爱华网
爱华网



