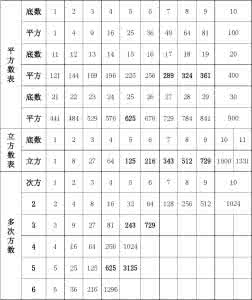
幂次数列
【例】-1,2,5,26,()
A.134 B.137 C.386 D.677
【答案】 D
【解题关键点】等差数列的平方加固定常数
【例】3,8,17,32,57,()
A.96 B.100 C.108 D.115
【答案】 B
【解题关键点】等差数列的平方加基本数列
平方数列变式。各项依次为+2,+4,+8,+16,+32,(+64),
其中每个数字的前项是平方数列,后项是公比为2的等比数列。
【例】343,216,125,64,27,()
A.8 B.9 C.10 D.12
【答案】A
【解题关键点】等差数列的立方
立方数列,分别为7,6,5,4,3,(2)的立方。
【例】4,9,25,49,121,()
A.144 B.169 C.196 D.225
【答案】B
【解题关键点】质数列的立方
各项依次写为,,,,,底数为连续质数,下一项应是=(169)。
【例】3,10,29,66,127,()
A.218 B.227 C.189 D.321
【答案】A
【解题关键点】等比数列的立方加固定常数
各项依分别为+2,+2,+2,+2,+2,(+2),也可以看作三级等差数列。
【例】2,10,30,68,(),222
A.130 B.150 C.180 D.200
【答案】A
【解题关键点】等比数列的立方加固定常数
各项依分别为+1,+2,+3,+4,+5,+6。
【例】4,13,36,(),268
A.97 B.81 C.126 D.179
【答案】A
【解题关键点】底数按基本数列变化
多次方数列变式。各项依次为4=+,13=+,36=+,(97)=(+),268=+
【例】,,1,3,4, ()
A.8 B.6 C.5 D.1
【答案】A
【解题关键点】指数按基本数列变化
=,=,1=,3=,4=,(1)=
【例】16,27,16,(),1
A.5 B.6 C.7 D.8
【答案】A
【解题关键点】底数和指数交错变化
对次方数列。16=,27=,16=,(5)=,1=
 爱华网
爱华网