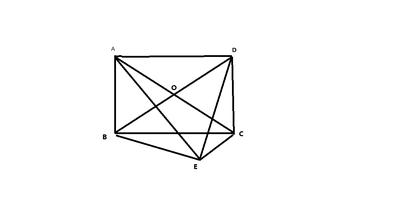
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,,。求CD的长和四边形ABCD的面积。题型:解答题难度:中档来源:北京中考真题
解:过D作DFAC于F如图,
∵,
∴、均为等腰直角三角形
∵DE=,
∴EF=DF=1,
∴CD=2DF=2, CF=,
又∵BE=2,
∴AB=AE=2,
S四ABCD=S△ABC+S△ACD
=AC(AB+DF)
=×(3+)×3
=
考点:
考点名称:等腰三角形的性质,等腰三角形的判定定义:有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。三角形的分类:
(1)三角形按边的关系分类如下:
;
(2)三角形按角的关系分类如下:
把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
 爱华网
爱华网



