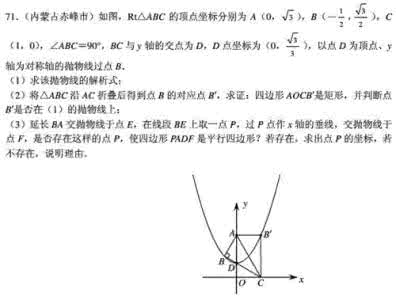
“抛物线模型”——抛物线的几何特征
图1
如图1,在平面直角坐标系中,点A的坐标是(0,2).在x轴上任取一点M,完成以下作图步骤:
①连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1,l2的交点为P.
②在x轴上多次改变点M的位置,用①的方法得到相应的点P,把这些点用平滑的曲线连接起来.
观察画出的曲线L,猜想它是我们学过的哪种曲线[i].
图2
图3
如图2、图3,通过几何画板软件演示,可以发现曲线L是二次函数的图象抛物线.
看视频演示。
高中课本中有以下的定义:平面内与一个定点F和一条定直线l(不经过定点F)距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线[ii].从几何方面揭示了抛物线的本质特征.那么我们就可以把图3中的点A称为焦点,x轴称为准线,而曲线L就是抛物线.
因此,我们可以得到以下结论:在平面内,必存在一个定点与一条定直线,使得抛物线上任意一点到它们的距离相等.如图4,点F(0,1),直线y=-1,点P在二次函数y=0.25x2的图象上,过点P作PH⊥直线y=-1 ,易得PF=PH.
图4
有了上面的结论,我们就可以进行试题的命制.从以往的中考试题中,常见的类型有与等边三角形的存在问题、最短路径问题等.
【典型例题】
(11眉山)如图,在直角坐标系中,已知点A(0,1),B(﹣4,4),将点B绕点A顺时针方向90°得到点C;顶点在坐标原点的拋物线经过点B.
(1)求抛物线的解析式和点C的坐标;
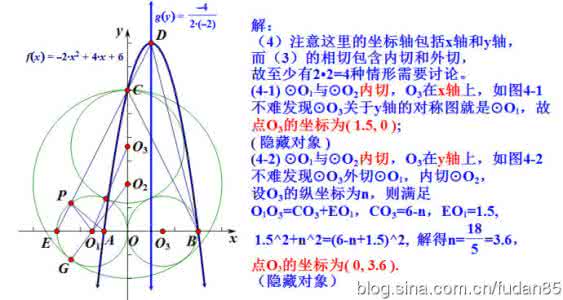
(2)抛物线上一动点P,设点P到x轴的距离为d1,点P到点A的距离为d2,试说明d2=d1+1;
(3)在(2)的条件下,请探究当点P位于何处时,△PAC的周长有最小值,并求出△PAC的周长的最小值.
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网!
 爱华网
爱华网