我们知道,一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移∣b∣个单位长度得到(当b>0时,向上平移;当b<0时,向上平移).或者说,直线y=kx平移∣b∣个单位长度得到直线y=kx+b (当b>0时,向上平移;当b<0时,向下平移).例如,将直线y=-x向上平移3个单位长度就得到直线y=-x+3,将直线y=-x向下平移1个单位长度就可以得到直线y=-x-1.需要注意的是,函数图象的平移,既可以上下平移,也可以左右平移.这里所说的平移,是指函数图象的上下平移,而非左右平移.
以上平移比较简单,因为它是对最简单的一次函数即正比例函数进行平移.对于一个一般形式的一次函数图象又该怎样进行平移呢?让我们一起进行探究:
问题1 已知直线:y=2x-3,将直线向上平移2个单位长度得到直线,求直线的解析式.
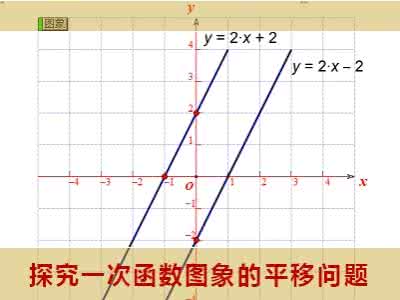
分析:根据“两直线平行,对应函数的一次项系数相等”,可设直线的解析式为y=2x+ b,由于直线的解析式中只有一个未知数,因此再需一个条件即可.怎样得到这个条件呢?注意到直线与两条坐标轴分别交于两点,而直线与y轴的交点易求,这样就得到一个条件,于是直线的解析式可求.
解:设直线的解析式为y=2x+b,直线交y轴于点(0,-3),向上平移2个单位长度后变为(0,-1).把(0,-1)坐标代入y=2x+b,得b=-1,从而直线的解析式为y=2x-1.
问题2 已知直线:y=2x-3,将直线向下平移2个单位长度得到直线,求直线的解析式.
答案:直线的解析式为y=2x-5.(解答过程请同学们自己完成)
对比直线和直线直线的解析式可以发现:将直线:y=2x-3向上平移2个单位长度得到直线的解析式为:y=2x-3+2;将直线:y=2x-3向下平移2个单位长度得到直线的解析式为:y=2x-3-2.(此时你有什么新发现?)
问题3 已知直线:y=kx+b,将直线向上平移m个单位长度得到直线,求直线的解析式.
简解:设直线的解析式为y=kx+n,直线交y轴于点(0,b),向上平移m个单位长度后变为(0,b+m),把(0,b+m)坐标代入的解析式可得,n=b+m.从而直线的解析式为y=kx+b+m.
问题4 已知直线:y=kx+b,将直线向下平移m个单位长度得到直线,求直线的解析式.
答案:直线的解析式为y=kx+b-m.(解答过程请同学们自己完成)
由此我们得到:直线y=kx+b向上平移m(m为正)个单位长度得到直线y=kx+b+m,直线y=kx+b向下平移m(m为正)个单位长度得到直线y=kx+b-m,这是直线直线y=kx+b上下(或沿y轴)平移的规律.
这个规律可以简记为:.
以上我们探究了直线y=kx+b的上下 (或沿y轴)的平移,如果直线y=kx+b不是上下(或沿y轴)平移,而是左右(或沿x轴)平移,又该怎样进行平移呢?Let,s go,让我们一起继续探究!
问题5 已知直线:y=3x-12,将直线向左平移5个单位长度得到直线,求直线的解析式.
简解:根据“两直线平行,对应函数的一次项系数相等”,可设直线的解析式为y=3x+b,直线交x轴于点(4,0),向左平移5个单位长度后变为(-1,0).把(-1,0)坐标代入y=3x+b,得b=3,从而直线的解析式为y=3x+3.
问题6 已知直线:y=3x-12,将直线向右平移5个单位长度得到直线,求直线的解析式.
答案:直线的解析式为y=3x-27.(解答过程请同学们自己完成)
对比直线和直线直线的解析式可以发现:将直线:y=3x-12向左平移5个单位长度得到直线的解析式为:y=3(x+5)-12;将直线:y=3x-12向右平移5个单位长度得到直线的解析式为:y=3(x-5)-12.(此时你有什么新发现?)
问题7 已知直线:y=kx+b,将直线向左平移m个单位长度得到直线,求直线的解析式.
简解:设直线的解析式为y=kx+n,直线交x轴于点(,0),向左平移m个单位长度后变为(0,-m),把(0,-m)坐标代入的解析式可得,n=km+b.从而直线的解析式为y=kx+km+b,即y=k(x+m)+b.
问题8 已知直线:y=kx+b,将直线向右平移m个单位长度得到直线,求直线的解析式.
答案:直线的解析式为y=k(x-m)+b.(解答过程请同学们自己完成)
由此我们得到:直线y=kx+b向左平移m(m为正)个单位长度得到直线y=k(x+m)+b,直线y=kx+b向右平移m(m为正)个单位长度得到直线y=k(x-m)+b,这是直线y=kx+b左右(或沿x轴)平移的规律.
这个规律可以简记为:
.
下面就请同学们运用一次函数图象平移的规律解决下面问题:
1.直线y=-x-3向上平移2个单位长度后得到的直线解析式是___;直线y=-2向下平移3个单位长度后得到的直线解析式是___.
2.直线y=-5x-12向左平移2个单位长度后得到的直线解析式是___;直线y=向右平移3个单位长度后得到的直线解析式是___.
3.直线y=8x+13既可以看作直线y=8x-3向___平移(填“上”或“下”)___单位长度得到;也可以看作直线y=8x-3向___平移(填“左”或“右”)___单位长度得到.
4.要由直线y=2x+12得到直线y=2x-6,可以通过平移得到:先将直线y=2x+12向___平移(填“上”或“下”)___单位长度得到直线y=2x,再将直线y=2x向___平移(填“上”或“下”)得到直线y=2x-6;当然也可以这样平移:先将直线y=2x+12向___平移(填“左”或“右”)___单位长度得到直线y=2x,再将直线y=2x向___平移(填“左”或“右”)得到直线y=2x-6;以上这两种方法是分步平移.也可以一次直接平移得到,即将直线y=2x+12向___平移(填“上”或“下”)直接得到直线y=2x-6,或者将直线y=2x+12向___平移(填“左”或“右”)直接得到直线y=2x-6.
参考答案:1.y=-x-1;y=+1
2.y=-5x-22;y=
3.上,16,左,2
4.下,12,下,6,右,6,右,3,下,18,右,9
2011-08-09 人教网关闭打印推荐给朋 爱华网
爱华网