巧虎的爱好是探险.听说切线山上有一个切线长定理隧道,巧虎决定只身前往探个究竟.同学们你是不是也很好奇啊?让我们一起追随巧虎,走进隧道看看有哪些险境吧!
巧虎走进切线长定理隧道,被精彩的概念所吸引,于是巧虎来到概念面前,静下心来细细咀嚼起这些概念来.
一、概念层层尽染隧道口
第一景:点与圆生成切线长──切线长定理的基本图形
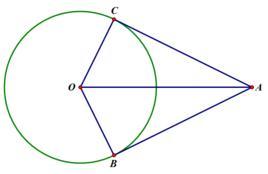
如图1所示,PA,PB是⊙O的切线,切点分别是A,B,则PA=PB,且∠APO=∠BPO.
这个定理可以引申如下结论:
三角形PAB 是等腰三角形,且OP垂直平分AB.希望同学们能够记住.
第二景:三角形与圆生成切线长
如图2所示,⊙I是三角形ABC 的内切圆,切点分别是D,E,F,则AD=AF,BD=BE,CE=CF.
如图3所示,当三角形ABC是等腰三角形时,点A ,I,E三点共线.
第三景:四边形与圆生成切线长
如图4所示,⊙I是四边形ABCD的内切圆,则AB+CD=AD+BC
二、点将训练场
第一供应点:点,圆中探求角大小
例1 (2010哈尔滨)如图5,PA、PB是⊙O的切线,切点分别是A、B,如果∠P=60°,那么∠AOB等于( ) A.60° B.90° C.120° D.150°
分析:根据切线的性质,知道∠PAO=∠PBO=90°,所以∠AOB+∠P=180°.因为∠P=60°,所以∠AOB=120°.解:选择C.
例2 如图6, 若AB、AC分别切⊙O于B、C,延长OB到D使BD=OB,连AD,如果∠DAC=78°,则∠ADO=( )A.56° B.39° C.64° D.78°
分析:根据切线长定理,知道∠BAO=∠CAO.因为AB切⊙O于B,所以∠ABO=∠ABD=90°.因为BD=OB,AB=AB,所以△ABO≌△ABD,所以∠BAO=∠BAD,所以∠BAD=∠DAC=26°,所以∠ADO=90°-26°=64°.解:选C.
第二供应点:三角形,圆中探求线段
1.一般三角形
例3 ⊙O内切于△ABC,切点分别是D、E、F,若AB=5,BC=6,AC=4.则BD=_____.
A 1.5 B 2.5 C 3.5 D 3
分析: 如图2所示,根据切线长定理,得到:AD=AF, BD=BE, CE=CF.
设AD=AF=x, BD=BE=y, CE=CF=z,BC=a,AC=b,AB=c,
则,解得AD=AF=, BD=BE=, CE=CF=,
所以BD=BE===3.5.解:选C.
点评: 请同学们熟记上面的三个小结论,对你解题一定会有很大的帮助的.
2.等边三角形
例4 (2010年兰州)如图7,正三角形的内切圆半径为1,那么这个正三角形的边长为( ) A 2 B 3 C D.2
分析: 当三角形是等边三角形时,三角形的内心与外心是重合的,所以OA是外接圆的半径,OD是内切圆的半径,且点D是边AB的中点,所以OD=1, ∠OAD=30°.在直角三角形AOD 中,
tan30°=,所以AD=,所以AB=2AD=2.解:选D.
点评: 设等边三角形的外接圆半径为R,内切圆的半径为r,边长为a,
则r:R:a=1:2:2.希望同学们能熟记这个结论.
3.直角三角形
例5 如图9所示,直角三角形ABC中,∠C=90°AB,BC,CA的长分别是c,a,b,求三角形ABC 内切圆的半径r.
分析: 此题是例3的一种特殊化,是把一般三角形变成了直角三角形.我们易证四边形IECF是正方形,所以z就等于内切圆的半径r,所以r=.
解:略.
引申: 内切圆的半径为r=.
解:因为∠C=90°AB,BC,CA的长分别是c,a,b,所以直角三角形的周长是a+b+c,=×BC×AC=ab.所以ab=r(a+b+c),所以内切圆的半径为r=.
第三供应点:等腰梯形,圆中探求线段
如图10,当四边形ABCD是等腰梯形时,我们会发现,它具有很多有趣的结论,下面我们就一一道来:
结论1:圆的外切等腰梯形的两底之和等于腰长的2倍.
简证:因为AB+CD=AD+BC,且AD=BC,所以AB+CD=2AD.
结论2:圆的外切等腰梯形的中位线等于腰长.
简证:设梯形的中位线为EF,因为AB+CD=AD+BC,且AD=BC,所以AB+CD=2AD.
因为AB+CD=2EF,所以AD=EF.
结论3:圆的外切等腰梯形的周长等于腰长的4倍.
简证:因为AB+CD=AD+BC,且AD=BC,所以AB+CD +AD+BC =2AD+2AD=4AD.
结论4:圆的外切等腰梯形的周长等于中位线的4倍.
简证:中位线等于腰长,所以结论是成立的.
结论5:切点G,E分别是CD,AB的中点.
简证:如图11,连接ID,IG,IC,则ID平分∠GDH,所以∠IDG=∠GDH .同理可证∠ICG=∠GCF.因为梯形ABCD是等腰梯形,所以∠GDH=∠GCF,所以∠IDG=∠ICG.
因为IG⊥DC,所以∠IGD=∠IGC.因为IG=IG,所以△IGD≌△IGC,所以GD=GC,即点G是CD的中点.同理可证点E是AB的中点.
结论6:圆的外切等腰梯形两底的积等于内切圆半径平方的4倍.
简证:如图12所示,连接ID,IH,IA,则ID平分∠GDH,所以∠IDH=∠GDH .同理可证∠IAH=∠DAB.因为AB∥CD,所以∠GDH+∠DAB=180°,
所以∠IDH+∠IAH=90°,所以∠AID=90°.
因为IH⊥AD,所以∠IHD=90°.所以△IDH∽△AIH,所以,所以.
因为DH=DG=CD,AH=AE=AB,所以AB×CD=4.
怎么样,这些结论你喜欢吗?当你熟记后,下面的小题你就会轻松拿下,试一试吧!
(1)一个等腰梯形的四条边都与一个圆相切,已知梯形的腰长为6cm,那么这个梯形的中位线长为( ) A、7cm B、6cm C、5.5cm D、5cm
(2)圆的外切等腰梯形周长为48cm,则它的腰长为( )
A、24cm B、12cm C、8cm D、6cm
(3)圆外切等腰梯形ABCD的中位线EF=15cm,则等腰梯形ABCD的周长是( )
A、15cm B、20cm C、30cm D、60cm
(4)四边形ABCD是⊙O的外切等腰梯形,若上底CD=4cm,圆的半径是3cm,
则腰长为 .
参考答案:
1 B 2 B 3 D 4 6.5
第四供应点:正方形,圆中探求线段
例6 如图13,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,再过A点作半圆的切线,与半圆相切于F点,与DC相交于E点.求:△ADE的面积.
分析: 要想求出三角形的面积,只要求出线段DE的长度即可.这里有两个关键点要注意,一个是BAF型切线长定理图,一个是CEF型切线长定理图.
解:因为AB,AF是圆O的切线,所以AB=AF.因为CE,EF是圆的切线,所以EF=EC.
设EF=EC=x,则AE=AF+EF=4+x,DE=CD-CE=4-x,
在直角三角形ADE中,
,所以,解得:x=1,
所以DE=CD-CE=4-x=3,所以三角形ADE的面积是:.
第五供应点:三角形,圆中探求面积
例7 三角形ABC的内切圆半径为r,三角形ABC的周长为,求三角形ABC 的面积.
分析: 求三角形面积的关键是利用内心的特点,巧妙分割三角形,采取化整为零的战术.
解: 如图14所示,设三角形内切圆的圆心为I,圆I与边AB,BC,CA的切点分别是D,E,F.连接IA,IB,IC ,ID ,IE,IF,因为D,E,F分别是切点,所以ID⊥IA,IE⊥IB,IF⊥IC,所以==×r×AB,==×r×BC,==×r×AC.因为=++,
所以=×r×AB+×r×BC +×r×AC=r(AB+BC+CA)=r.
巧虎经历了这次探险,更加激发了他学习数学热情,他决心要把数学学好,立志长大成为一名数学家.
作者简介:左效平,中学数学高级教师,山东省沂源县徐家庄中心学校副校长,擅长解题方法的探究和学法指导的归纳总结,在《中学生数理化》《中学数学杂志》《数学周报》《数理报》《数理天地》《中学生》等杂志,报刊刊发论文近百篇,在“希望杯”数学竞赛中获得命题奖二等奖,沂源县数学中心教研组成员。
 爱华网
爱华网


