二轮复习专题讲座:集合与简易逻辑、函数与导数部分
第1讲 集合的基本概念与运算
第2讲 简易逻辑
第3讲 函数的概念与性质
【典型例题】
二. 知识分析:
第1讲 集合的基本概念与运算
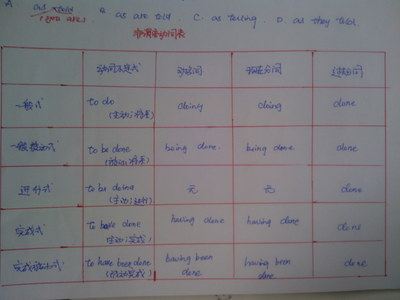
例1. 指出下列几个集合的异同处
解:集合A是指指数函数的定义域,;
集合B是指指数函数的值域,
集合C是指指数函数的图像上所有的点构成的集合,是一个点集;
集合D是一个单元素集合,这个元素是一个方程;
集合A、B、C是描述法表示集合,集合D是列举法表示集合。
例2. 设集合,,则集合中元素的个数为( )
A. 1 B. 2 C. 3 D. 4
解:选B.如上图,在同一坐标系画出两个点集所表示的图象.由图象可知,两曲线有两个交点,即有两个元素.
例3. 设、为两个非空实数集合,定义集合,若,则中元素的个数是_______________.
解:因为,所以.当时,分别取1,2,6可得分别为1,2,6;当时,分别取1,2,6可得分别为3,4,8;当时,分别取1,2,6可得分别为6,7,11.综上:,故中有8个元素.
例4. 已知集合,,若,则实数的取值构成的集合为______________________.
解:方程两根分别为:,因此.
由得或{2}或{-3},
所以,实数的取值构成的集合为.
例5. 已知,二次函数.设不等式的解集为A,又知集合,若,求的取值范围.
解:易知,由得:,,
由此可得:.
(1)当时,,的充要条件是,
即,解得;
(2)当时,,的充要条件是,
即,解得.
综上所述,使成立的的取值范围为.
例6. 设集合A中不含有元素-1,0,1,且满足条件:若,则有,请考虑以下问题:(Ⅰ)已知,求出A中其它所有元素;
(Ⅱ)自己设计一个实数属于A,再求出A中其它所有元素;
(Ⅲ)根据已知条件和前面(Ⅰ)(Ⅱ)你能悟出什么道理来,并证明你的猜想.
解:(Ⅰ)由,则,
所以集合;
(Ⅱ)任取一常数,如3,则同理(Ⅰ)可得:;
(Ⅲ)猜想任意的,则集合.
下面作简要证明:
,则.
这四个元素互不相等,否则.
第2讲 简易逻辑
例1. 直线与平行(不重合)的充要条件是( )
A. B. C. D. 或
解:,所以;故选C.
例2. 命题p:若、∈R,则是的充要条件;
命题q:函数的定义域是则( )
A. “p或q”为假 B. “p且q”为真
C. p真q假 D. p假q真
解:由三角形不等式知:是的必要不充分条件,即p为假命题;由可得或,即为真命题.故选D.
例3. 在空间中:①若四点不共面,则这四点中任何三点都不共线;②若两条直线没有公共点,则这两条直线是异面直线.以上两个命题中逆命题为真命题的是 .
解:①的逆命题为:若四点中任何三点都不共线,则这四点不共面.例如:正方形的四个顶点不共线但共面,故其不正确;②的逆命题为:若两条直线是异面直线,则这两条直线没有公共点.由异面直线定义知,异面直线没有公共点,故②的逆命题为真命题.
例4. 已知;?是?的必要不充分条件,求实数的取值范围.
解:由得,
由,得,
∴?即,或,而?即,或;
由?是?的必要不充分条件,知?,
设A=,B=,
则有A,故且不等式中的第一、二两个不等式不能同时取等号,
解得,此即为“?是的必要不充分条件”时实数的取值范围。
例5. 已知条件和条件,请选取适当的实数的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题。则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题。
解:已知条件即,或,∴,或,
已知条件即,∴,或;
令,则即,或,此时必有成立,反之不然.
故可以选取的一个实数是,A为,B为,对应的命题是若则,
由以上过程可知这一命题的原命题为真命题,但它的逆命题为假命题.
例6. 已知p:是的反函数,且;
q:集合,B = { x | x >0},且AB=.
求实数a的取值范围,使“p或q”为真命题,“p且q”为假命题.
解:先考虑:∵是f (x )=1-3x的反函数,∴,由,可得,解得:;
再考虑:①当△<0时,,,此时:由得;
②当△≥0时,由可得:,解得.
由①②可知.
要使p真q假,则;要使p假q真,则,综上所述,当的范围是时,p、q中有且只有一个为真命题.
第3讲 函数的概念与性质
例1. 设,则的定义域为( )
A. B.
C. D.
解:∵在中,由,得, ∴,
∴的定义域满足,.
故选B.
例2. 已知是上的减函数,那么a的取值范围是( )
A. (0,1) B. C. D.
解:∵是上的减函数,
当时,,∴;
又当时,,∴,∴,
且,解得:.
∴综上,,故选C.
例3. 函数对于任意实数满足条件,若,则 .
解:∵函数对于任意实数满足条件,
∴,即的周期为4,
∴,
∴.
例4. 设的反函数为,若,则 .
解:∵,∴.
例5. 已知是关于的方程的两个实根,则实数为何值时,大于3且小于3?
解:令,
则方程的两个实根可以看成是
抛物线与轴的两个交点(如图所示),故有:,
所以:,解之得:.
例6. 定义在上的奇函数满足,且当时,有
(1)求证:是上的增函数;
(2)证明:当时,
解:(1)任取,且,
则
因为,所以
所以,是上的增函数。
(2)由(1)可知:当时,,
所以,当时,
【模拟试题】
1、已知,则( )
A. B.
C. D.
2、设集合,,
,那么满足点P(2,3)条件是( )
A. m>—1,n<5 B. m<—1,n<5
C. m>—1,n>5 D. m<—1 ,n>5
3、不等式的解集为Q,,若,则( )
4、“”是“直线与圆相切”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分又不必要条件
5、不等式成立的一个必要而不充分条件是( )
A. B. C. D.
6、给出下列三个命题:
①若,则;
②若正整数m和n满足,则;
③设为圆上任一点,圆O2以为圆心且半径为1.当时,圆O1与圆O2相切.
其中假命题的个数为 ( )
A. 0 B. 1 C. 2 D. 3
7、函数的反函数是( )
A. B.
C. D.
8、是定义在R上的偶函数,是奇函数,又知,且,则的值是 ( )
A. 150 B. -150 C. 2008 D. -2008
9、若函数,则该函数在上是( )
A. 单调递减无最小值 B. 单调递减有最小值
C. 单调递增无最大值 D. 单调递增有最大值
10、函数,若,则的所有可能值为( )
A. 1 B. C. 1, D. 1,
11、已知集合,若AB =,则实数P的取值范围是______________________.
12、定义运算: 则函数的值域为 .
13、已知在其定义域上为增函数,,则不等式的解集是_________________
14、以下同个关于圆锥曲线的命题中:
①设A、B为两个定点,k为非零常数,,则动点P的轨迹为双曲线;
②设定圆C上一定点A作圆的动点弦AB,O为坐标原点,若则动点P的轨迹为椭圆;
③方程的两根可分别作为椭圆和双曲线的离心率;
④双曲线与椭圆有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
15、集合,,且,求实数a的取值范围.
16、设集合,,问是否存在非零整数,使?若存在,请求出的值及;若不存在,请说明理由.
17、已知设:函数在R上单调递减;:不等式的解集为R.如果p或q为真,p且q为假,求的取值范围.
18、定义在R上的奇函数有最小正周期2,且时,.
(1)求在[-1,1]上的解析式;
(2)判断在(0,1)上的单调性,并给予证明.
【试题答案】
1、A 2、A 3、B 4、A 5、D 6、B 7、A 8、B 9、C 10、C
11、 12、 13、 14、③④
15、解:
(1)当时,,满足;
(2)当时,是二次函数,
若,,则;
若,;
由得,
综合(1)(2)得.
16、由知,a是否存在,取决于方程组是否有x的正整数解,
消去y得:①,
由,即,解得.
因为a为非零整数,所以a可能取的值为.
当时,代入①解得,这与矛盾,故;
当时,代入①解得,符合题意.
所以存在,使得,此时.
17、对于命题p:函数在R上单调递减;对于命题q:不等式的解集为R函数,所以函数在R上最小值为,故不等式的解集R.
由“p或q为真,p且q为假”p、q中一真一假.如果p 真q假,即,
解得;如果p假q真,即,解得,综上的取值范围为.
18、(1)当时,,
∵为奇函数,∴,
又,,,
∴.∴
(2)在(0,1)上是减函数。
下面证明:任取且,
因为。
由于,则,则,
由知,即,
所以,即,所以在(0,1)上为减函数.
 爱华网
爱华网