[学习目标]
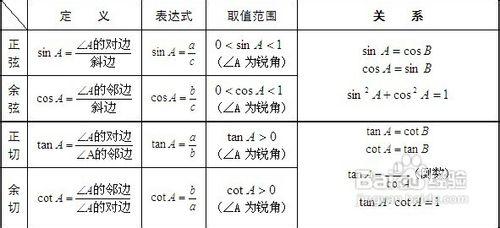
1. 正确记忆理解四个锐角三角函数
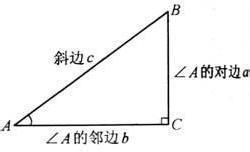
(1)正弦:在直角三角形中,一个锐角所对的直角边与斜边的比,叫这个锐角的正弦。
即:如图1
(2)余弦:在直角三角形中,一个锐角的邻边与斜边的比,叫这个锐角的余弦。
即:如图1
(3)正切:在直角三角形中,一个锐角所对的直角边与相邻直角边的比,叫这个锐角的正切。
即:如图1
(4)余切:在直角三角形中,一个锐角相邻的直角边与所对的直角边的比,叫这个锐角的余切。
即:如图1
2. 特殊角的三角函数值:
3. 互余两角正、余弦间的关系;正、余切间的关系。
(1)任意锐角的正弦值,等于它余角的余弦值;任意锐角的余弦值等于它余角的正弦值。
即:
(2)任意锐角的正切值等于它余角的余切值;任意锐角的余切值等于它余角的正切值。
即:
4. 同角的正、余弦间的关系;正、余切间的关系;四个锐角三角函数间的关系。
(1)
当0°<A<45°,;
当45°<A<90°,。
(2)
当0°<A<90°时,正切值随角度的增加(减少)而增加(减少)。
当0°<A<90°时,余切值随角度的增加(减少)而减少(增加)。
(3)
二. 重点、难点:
重点理解锐角三角函数定义,培养用其解题意识,掌握锐角三角函数的性质。
难点是应用锐角三角函数定义解边角关系及辅助线的添加。
【典型例题】
例1. 已知△ABC,∠C=90°,a=3,c=4,求∠A的四个三角函数值。
解:∵∠C=90°
∴△ABC为Rt△ABC
在Rt△ABC中,根据勾股定理:
例2. 已知△ABC,∠C=90°,,求cosA,b,c的值。
解:在中,∠C=90°,
在中,由勾股定理:
(舍去)
例3. 已知△ABC,∠C=90°,,求tanA的值。
解:在中,∠C=90°,
(舍去)
例4. 已知△ABC,∠C=90°,,求∠A的四个三角函数值。
解:在中,∠C=90°
∴可设
在,由勾股定理:
(舍去)
例5. 已知:如图2,△ABC中,∠A=90°,AB=AC,AD:DC=1:2,求∠DBC的四个三角函数值。
解:过点D作DH⊥BC于H
∵AD:DC=1:2
∴可设AD=k,DC=2k
∴,△ABC是等腰三角形
∵∠A=90°
∴△ABC是等腰直角三角形
∴∠C=45°
在Rt△ABD中,由勾股定理:
∵DH⊥BC于H
∴∠DHC=90°
∴△DHC是等腰直角三角形
∵∠C=45°,DC=2k
在中,
∵∠C=45°,AC=3k
∴在中
例6. 已知:如图3,在△ABC中,AB=AC,∠A=90°,。
求证:∠AED=∠DBC
证明:
∴可设
则
∵在中,
∴∠C=45°
∴过点D作DH⊥BC于H
在中,
同理,
同理,在中,
在中,
例7. 已知:如图4,在△ABC中,∠C=90°,CD⊥AB于D,DE⊥AC于E。
求证:
证明:∵CD⊥AB于D
∴∠CDA=90°
∴△ACD为Rt△ACD
∴∠1与∠A互余
同理,∠1与∠2互余
∴∠2=∠A
∵DE⊥AC于E
∴∠DEA=90°
∴△DAE为Rt△DAE
∴在中,
同理,在中
即:
在中,∠C=90°
例8. 计算:
(1)
(2)
(3)
(4)已知(为锐角,求的值)
解:(1)
(2)
(3)
(4),为锐角
例9. 计算:
(1)
(2)
(3)
解:(1)
(2)
(3)原式
【模拟试题】(答题时间:40分钟)
一. 选择题。
1. 在中,∠C=90°,AC=15,BC=8,则sinA与sinB的值是( )
A. B.
C. D.
2. 在等腰△ABC中,AB=AC=10cm,BC=12cm,则的值是( )
A. B. C. D.
3. 在中,∠C=90°,,则sinB的值是( )
A. B. C. D.
4. 等腰△ABC中,AB=AC=3cm,BC=2cm,则tanB,的值是( )
A. B.
C. D.
5. 已知,则的值是( )
A. 1 B. C. D. 2
二. 填空题。
6. 若α为锐角,且,则=________。
7. __________。
8. __________。
9. ,则__________。
,α为锐角,则α=_________。
10. ,则锐角A、B关系是____________。
11. ___________。
12. 锐角A满足,则__________。
三. 解答题。
13. 如图5,已知等腰△ABC中,AB=AC=10,BC=12,求sinB,cosB的值。
图5
14. 如图6,在中,CD是斜边上的高,已知,求sin∠ACD与cosB。
15. 计算:
(1)
(2)
(3)
(4)
【试题答案】
一. 选择题。
1. A 2. A 3. C 4. D 5. B
二. 填空题。
6. 67° 7. 1 8. 1
9. 0.8643, 10. 相等
11. 1 12. 6
三. 解答题。
13. 解:作AD⊥BC于D
∵AB=AC,AD⊥BC
∴
∴在中
14. 解:在中,由勾股定理:
15. (1);(2);(3);(4)
【励志故事】
乘奇而入
45年前,联邦德国的福斯汽车公司准备入主美国汽车大市场,此前曾派出大批人马做了一番细致入微的市场调查研究。在调研中了解到:美国人最大的天性之一就是争强好胜,喜欢标新立异。
于是,他们特意设计生产出了一种造型奇特,犹如“金甲虫”状的微型小卧车,当年就畅销40余万辆,打开了美国汽车营销大市场,增加了人们对福斯汽车的认可度。
 爱华网
爱华网