岩瑞中学 七年级数学竞赛试题 岩瑞中学2013-2014学年七年级竞赛模拟数学试题

岩瑞中学2013-2014学年七年级竞赛模拟数学试题

姓名：____________ 得分：___________

一、选择题（共8小题，每小题5分，满分40分．以下每小题有且只有一个选项是正确的．请将

正确选项的代号填入题后的括号里）

1、 计算: (－4)2010×(－0.25)2011＝„„„„„„„„„„„„ ( )

A、－4 B、－1 C、－0.25 D、－2011

2、设“●，▲，■”分别表示三种不同的物体，如下图所示，前两架天平保持平衡，如果要使第三架天平也平衡，那么“？”处应放“■”的个数为„„„„„„„„( )

(1) (2) (3) A、5 B、4 C、3 D、2

3、在高速公路上，从3千米处开始，每隔4千米经过一个限速标志牌；并且从10千米处开始，每隔9千米经过一个速度监控仪。刚好在19千米处第一次同时经过这两种设施，那么第二次同时经过这两种设施的千米数是„„„„„„„„„„„„„„„„( )

A、55 B、67 C、106 D、127

4、如图，正方形ABCD的边长是3cm，一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转，那么这个小正方形第一次回到起始位置时，它的方向

是„„„„„„„„„„„„„„„„„„„„„„„„„„„„„„„„ ( )

A

B、

C D

A'

A

B'

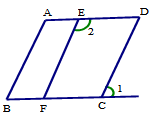
(第4题图) (第8题图) 5、如图，把△ABC绕点C顺时针旋转B′C，A′B′交AC于D，已知

o∠A′DC＝80，若AB与A′B′交与E，则∠BEA′的度数是„„„„„„„ ( )

A、135o B、 145o C、155o D、165o

6、适合│2a+7│+│2a-1│=8的整数a的值的个数有 „„„„„„„„„„„„„ ( )

A、2 B、4 C、8 D、16

76倍，还剩下一个小组在教室里讨论问题，这一小组是„ ( )

A、第4组 B.、第6组 C 、第7组 D、第11组

8、甲、乙、丙、丁、戊五位同学参加一次节日活动，很幸运的是他们都得到了一件精美的礼品（如图），他们每人只能从其中一串的最下端取一件礼品，直到礼物取完为止，甲第一个取得礼物，然后乙、丙、丁、戊依次取得第2到第5件礼物，他们的取法各种各样.，发现礼物D最精美，那么取得礼物D可能性最大的是同学是 „„„„„„„ ( )

A、乙 B、丙 C、丁 D、戊

二、填空题(每小题5分，共40分)

9、定义a*b=ab+a+b,若3*x=27，则x的值是_____。

10、三个有理数ａ、ｂ、ｃ之积是负数，其和是正数，当x＝

x1992x2______。 aabbcc时，则

11、当整数m＝_________ 时，代数式6的值是整数。 3m1

12、A、B、C、D、E、F六足球队进行单循环比赛，当比赛到某一天时，统计出A、B、C、D、E、五队已分别比赛了5、4、3、2、1场球，则还没与B队比赛的球队是______ 。

x13、甲从A地到B地，去时步行，返回时坐车，共用x小时，若他往返都座车，则全程只需3时，，若他往返都步行，则需____________小时。

14、李志明、张斌、王大为三个同学毕业后选择了不同的职业，三人中只有一个当了记者。一次有人问起他们的职业，李志明说：“我是记者。”张斌说：“我不是记者。”王大为说：“李志明说了假话。” 如果他们三人的话中只有一句是真的， 那么_______是记者。

1111_______. 15、12233420062007

16、若正整数x，y满足2004x＝15y，则x＋y的最小值是_______________

三、解答题(每小题10分，共40分)

17（10分）、现将连续自然数1至2009按图中的方式排列成一个长方形队列，再用正方形任意框出16个数。

1 2 3 4 5 6 7 8 9 10 11 12 13 14

15 16 17 18 19 20 21 22 23 24 25 26 27 28 · · · · · · · 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009

（1）设任意一个这样的正方形框中的最小数为n，请用n的代数式表示该框中的16个数，然后填入右表中相应的空格处，并求出这16个数中的最小数和最大数，然后填入右表中相应的空格处，并求出这16个数的和。（用n的代数式表示）

（2）在图中，要使一个正方形框出的16个数之和和分别等于832、2000、2008是否可能？若不可能，请说明理由；若可能，请求出该正方形框出的16个数中的最小数和最大数。

18（10分）、袋中装有大小相同的黑球、白球、红球各2个。规定：取出一个黑球记0分，取出一个白球记1分，

取出一个红球记2分；在抽取这些球的时候，看不到球的颜色。甲先取出3个球，不再放回袋中，然后，乙取出剩余的3个球；取出球的总积分多者获胜。

（1）甲获胜的概率是多少？

（2）甲、乙成平局的概率为多少？

19（10分）、如图1，点O为直线AB上一点，过O点作直线OC，使∠BOC=120°，将一直角三角板的直角顶点

放在O处，一边OM在射线OB上，另一边ON在直线AB下方。（10分）

（1）将图1中的三角板绕点O按顺时针方向旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC。

问：直线ON是否平分∠AOC？请说明理由。（4分）

（2）将图1中的三角板绕点O按每秒6°的速度逆时针方向旋转．

①若旋转一周，在旋转过程中，直线ON恰好平分∠AOC时，求旋转的时间t值。（4分）

②若旋转到某一时刻，使ON在∠AOC的内部，且∠AOM=3∠NOC，求旋转的时间值。（4分）

20（10分）、甲、乙二人在同一条椭圆形跑道上作特殊训练：他们同时从同一地点出发，沿相反方向跑，每人跑完第一圈到达出发点后立即回头加速跑第二圈，跑第一圈时，甲的速度为每分钟60米，乙的速度是甲速度的甲跑第二圈时速度比第一圈提高了N

图1

2，311，乙跑第二圈时速度提高了. 已知甲、乙二人第二次相遇点距第一次相遇35

点190米，问：这条椭圆形跑道长多少米？

七年级数学竞赛参考答案

一、选择题

1、C 2、A 3、A 4、A 5、C 6、B 7、D 8、B 二、填空题：

9、6 ; 10、-89 ; 11、 0 ，1 ; 12、 E ;

5200613、 x ; 14 、张斌; 15、 ; 16、673.

32007

三、解答题：

17、 （1）、 n n+1 n+2 n+3 n+7 n+8 n+9 n+10 n+14 n+15 n+16 n+17 n+21 n+22 n+23 n+24

这16个数的和=16n+192=16（n+12）

（2）、设 16（n+12）=832 n=40 ∴存在最小为40，最大40+24=64

16（n+12）=2000 n=113 ∴存在最小为113，最大为137， 16（n+2）=2008 n=125.5， ∴不存在。

18

得

甲、乙两人一轮取球共得6分。

63 20582 （2）甲得3分，则乙也得3分，两人成平局，概率为

205

（1）列表看出，甲获胜须得分为4、5或6分，概率为19、解：（1）如图1，直线ON平分∠AOC， ∵∠BOC=120°，OM平分∠BOC， ∴∠MOB=∠MOC=60°， 又∵∠MON=90°， ∴∠NOB=30° ∴∠AOD=30° ∴∠COD=30°

即∠AOD=∠COD，直线ON平分∠AOC

（2）t的值为6024010秒或80秒； 66（3）如图2，ON在∠AOC的内部，

且∠AOM=3∠NOC

∵∠AOM+∠AON=90°

∠CON+∠AON=60°

∴∠AOM－∠CON=30

∴∠CON=15°，旋转角为225°，t

22537.5 6

20、解：一开始甲的速度为每分钟60米，乙的速度为每分钟40米，设跑道长为x米，再设第一次相遇时需t1分钟。

xx分钟， 6040100

32则第一次相遇时甲跑为x米，乙跑了x米， 55

22114x分钟，此时乙又跑了x40x米，离出发点还有甲跑完余下的x米，需x605515015015

241(1)xx米， 5153

111x分钟，此时甲已经以每分钟80米的速度 乙跑完余下的x米，需x4033120

121x80x米，此时乙也以每分钟48米的速度折返，且两相相距x米， 折返12033

1x111x48x米， 第二次相遇需t2x分钟，乙又跑了3128880483128

3119x米， 二次相遇点间的距离为xx5840

19x190，x400米， 即40t1

答：跑道长为400米

爱华网本文地址 » http://www.aihuau.com/a/356551/142434666408.html