四面体有不同的名字,四面体,三棱锥,空间四边形加上两条对角线等。三角形和四面体,关系一直很微妙。从地位上说,三角形是边数最少的平面多边形,四面体是面数最少的空间多面体;从性质上看,三角形的很多性质都能在四面体里找到类似的性质。比如三角形必有外接圆和内接圆,四面体也必有外接球和内接球等。今天学夫子就将这两个几何体类似的性质做一个总结,方便大家的需要。
一:三角形的两边之和大于第三边
这条性质应该再熟悉不过吧,他直观地表述了两点之间直线距离最短的道理。这条性质反映到四面体中就有了两条类似的结论:
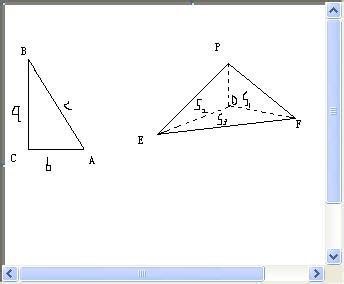
1:四面体三个面的面积之和大于第四个面
这条性质的直观意义是很明显的,当然也能证明,做A点在面BDC上的投影,利用一个面的投影比平面面积小来证明即可,就好像证明一条线段在另一条直线上的投影比原直线短一样。
2:同一顶点的三个角中,两角之和大于第三角
如图所示,角ABD+角ABC>角BDC。这其实就是三面角的性质,我们也可以通过做线段AB在面BDC上投影的办法来证明。这条性质的用处是很大的,比如证明《若三角形按中位线能折叠成四面体,则该三角形一定为锐角三角形》,用到的核心性质就是这一条,详情请参见该文。
二:勾股定理
直角三角形有一个家喻户晓的勾股定理,四面体也有类似的性质:
若在四面体中同一顶点的三个面互相垂直,则垂直面的面积平方之和等用于第四边的面积平方,如图,若面ABP⊥面APC⊥面ABC,则有S2(ABP)+S2(APC)+S2(ABC)=S2(BDC).你可以将之看成是勾股定理在三维空间的推广,不过其正面要用到勾股定理及其相关结论。
三:余弦定理正弦定理
这也是三角形的著名定理,余弦定理相比勾股定理,更具普适性。反映在空间几何里就是:
而正弦定理当然也有,非常类似三角形的正弦定理:
四:正三角形内一点到各边距离之和为一常数
这个性质反映到正四面体里就是:正四面体内一点到各边的距离之和为一常数,关于这一点及其详细内容,我在《从一个等边三角形性质想起》一文里介绍过。
五:中线定理
你也可以将之叫做重心定理,其物理和数学意义都非常明显。重心就是这一点的物理学中心,如果三角形质地均匀的话,这一点就是所谓的平衡点,如果学夫子在这里将一维直线到二维三角形再到三维四面体的重心及其性质放在一起的话,相信更能引起您的遐想了:
你会不会因此想把这个结论推广到想象不到的“高维空间”呢?当然,如果你考虑重心的物理性质,利用力的原理去解决的话,那么这一切将变得很简单。(来源:学夫子数学博客)
 爱华网
爱华网