教学目标:
1. 能够写出实际问题中反比例关系的函数解析式,从而解决实际问题。
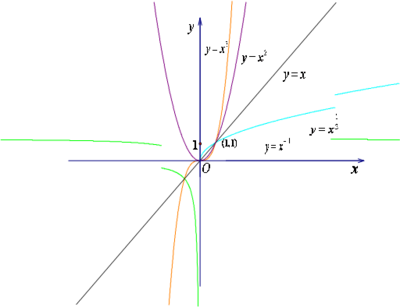
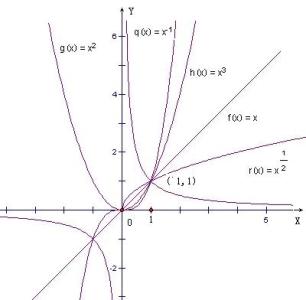
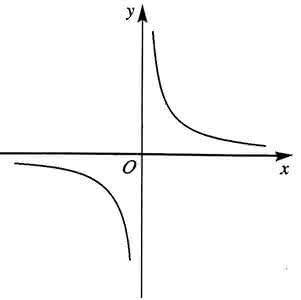
2. 用描点法画出反比例函数的图象,当时,双曲线的两支在一、三象限;当时,双曲线的两支在二、四象限,双曲线是关于原点的对称图形,这一点在作图时很重要。
3. 用一元方程求解反比例函数的解析式,学习中与正比例函数相类比。
4. 掌握反比例函数增减性,时,y随x的增大而减小,时,y随x的增大而增大。
5. 熟练反比例函数有关的面积问题。
二. 重点、难点
重点:反比例函数的定义、图象性质。
难点:反比例函数增减性的理解。
【典型例题】
例1. 下列各题中,哪些是反比例函数关系。
(1)三角形的面积S一定时,它的底a与这个底边上的高h的关系;
(2)多边形的内角和与边数的关系;
(3)正三角形的面积与边长之间的关系;
(4)直角三角形中两锐角间的关系;
(5)正多边形每一个中心角的度数与正多边形的边数的关系;
(6)有一个角为的直角三角形的斜边与一直角边的关系。
解:成反比例关系的是(1)、(5)
点拨:若判断困难时,应一一写出函数关系式来进行求解。
例2. 在同一坐标系中,画出和的图象,并求出交点坐标。
点悟:的图象是双曲线,两支分别在一、三象限,在每一个象限内,y随x的增大而减小。并且每一支都向两方无限接近x、y轴。而的图象是过原点的直线。
解:
,
双曲线与直线相交于(2,4),()两点。
点拨:本题求解使用了“数形结合”的思想。
例3. 当n取什么值时,是反比例函数?它的图象在第几象限内?在每个象限内,y随x增大而增大或是减小?
点悟:根据反比例函数的定义:,可知是反比例函数,必须且只需且
解:是反比例函数,则
即
故当时,表示反比例函数
双曲线两支分别在二、四象限内,并且y随x的增大而增大。
点拨:判断一个函数是否是反比例函数,惟一的标准就是看它是否符合定义。
例4. 若点(3,4)是反比例函数图象上一点,则此函数图象必经过点( )
A. (2,6) B. (2,-6)
C. (4,-3) D. (3,-4)
(2002年武汉)
点悟:将点(3,4)代入函数式求出m的值。
解:将点(3,4)代入已知反比例函数解析式,得
即,
将A点坐标代入满足上式,故选A。
点拨:本题中求的值的整体思想是巧妙解题的关键。
例5. a取哪些值时,是反比例函数?求函数解析式?
解:
解得,
当时,
当时,
当时,函数是反比例函数,其解析式为
点拨:反比例函数可写成,在具体解题时应注意这种表达形式,应特别注意对这一条件的讨论。
例6. 若函数是反比例函数,求其函数解析式。
解:由题意,得
得
故所求解析式为
点拨:在确定函数解析式时,不仅要对指数进行讨论,而且要注意对x的系数的条件的讨论,二者缺一不可。
例7. (1)已知,而与成反比例,与成正比例,并且时,;时,,求y与x的函数关系式;
(2)直线:与平行且过点(3,4),求的解析式。
解:(1)与成反比例,与成正比例
,
把,及,代入
得
(2)与平行
又过点(3,4)
,
直线的解析式为
点拨:这是一道综合题,应注意综合应用有关知识来解之。
例8. 一定质量的二氧化碳,当它的体积时,它的密度
(1)求与V的函数关系式;
(2)求当时二氧化碳的密度。
解:(1)由物理知识可知,质量m,体积V,密度之间的关系为。由,,得
(2)将代入上式,得
点拨:这是课本上的一道习题,它具有典型性,其意义在于此题与物理知识、化学知识形成了很好的结合,且V的取值可变化。
例9. 在以坐标轴为渐近线的双曲线上,有一点P(m,n),它的坐标是方程的两个根,求双曲线的函数解析式。
点悟:因为反比例函数的图象是以坐标轴为渐近线的双曲线。所以,不妨设所求的函数解析式为。然后把双曲线上一点的坐标代入,即可求出k的值。
解:由方程解得
,
P点坐标为()或()
设双曲线的函数解析式为,则
将,代入,得
将,代入,得
故所求函数解析式为
点拨:只需知道曲线上一点即可确定k。
例10. 如图,的锐角顶点是直线与双曲线在第一象限的交点,且
(1)求m的值
(2)求的值
解:(1)设A点坐标为(a,b)(,)
则,
,
又A在双曲线上
,即,
(2)点A是直线与双曲线的交点
或
A()
由直线知C(-6,0)
,,
点拨:三角形面积和反比例函数的关系,常用来求某些未知元素(如本例中的m)
【模拟试题】(答题时间:40分钟)
一. 选择题
1. 函数是反比例函数,则m的值是( )
A. 或 B.
C. D.
2. 下列函数中,是反比例函数的是( )
A. B.
C. D.
3. 函数与()的图象的交点个数是( )
A. 0 B. 1 C. 2 D. 不确定
4. 函数与的图象可能是( )
A B C D
5. 若y与x成正比,y与z的倒数成反比,则z是x的( )
A. 正比例函数 B. 反比例函数
C. 二次函数 D. z随x增大而增大
6. 下列函数中y既不是x的正比例函数,也不是反比例函数的是( )
A. B.
C. D.
二. 填空题
7. 一般地,函数__________是反比例函数,其图象是__________,当时,图象两支在__________象限内。
8. 已知反比例函数,当时,_________
9. 反比例函数的函数值为4时,自变量x的值是_________
10. 反比例函数的图象过点(-3,5),则它的解析式为_________
11. 若函数与的图象有一个交点是(,2),则另一个交点坐标是_________
三. 解答题
12. 直线过x轴上的点A(,0),且与双曲线相交于B、C两点,已知B点坐标为(,4),求直线和双曲线的解析式。
13. 已知一次函数与反比例函数的图象的一个交点为P(a,b),且P到原点的距离是10,求a、b的值及反比例函数的解析式。
14. 已知函数是一次函数,它的图象与反比例函数的图象交于一点,交点的横坐标是,求反比例函数的解析式。
【试题答案】
一. 1. B 2. B 3. A 4. A 5. A 6. C
二. 7. ,;双曲线;二、四
8. 9. 10. 11. (,)
三. 12. 由题意知点A(,0),点B(,4)在直线上,由此得
点B(,4)在双曲线上
,
双曲线解析式为
13. 由题设,得
,
,或,
14. 由已知条件
使
代入
因图象交于一点,
即
【励志故事】
愚钝的力量
大科学家爱因斯坦曾做过一个实验:他从村子里找了两个人,一个愚钝且软弱,一个聪明且强壮。爱因斯坦找了一块两英亩左右的空地,给他俩同样的工具,让他们在其间比赛挖井,看谁最先挖到水。
愚钝的人接到工具后,二话没说,便脱掉上衣干起来。聪明的人稍作选择也大干起来。两个小时过去了,两人均挖了两米深,但均未见到水。聪明的人断定选择错了,觉得在原处继续挖下去是愚蠢的,便另选了块地方重挖。愚钝的人仍在原地吃力地挖着,又两个小时过去了,愚钝的人只挖了一米,而聪明的人又挖了两米深。愚钝的人仍在原地吃力地挖着,而聪明的人又开始怀疑自己的选择,就又选了一块地方重挖。又两个小时过去了,愚钝的人挖了半米,而聪明的人又挖了两米,但两人均未见到水。这时聪明人泄气了,断定此地无水,他放弃了挖掘,离去了。而愚钝的人此时体力不支了,但他还是在原地挖,在他刚把一锨土掘出时,奇迹出现了,只见一股清水汩汩而出。
比赛结果,这个愚钝的人获胜。爱因斯坦后来对学生说,看来智商稍高、条件优越、聪明强壮者不一定会得到成功,成功有时需要一种近乎愚钝的力量啊!
 爱华网
爱华网