在有些二元函数求最值的问题中,构建向量模型,常常会使复杂的问题变得简洁明了,利用向量的坐标及向量的内积,会使繁琐的解题过程显得巧妙与自然,下面举例进行分析:
例1:已知:,求的最大值。
解:由已知,可取一定点M(3,2)
设N(x,y)为圆上任意一点,0为原点,
则OM=(3,2),ON=(x,y)
所以
那么
的最大值为
例2:已知:,求的最小值。
解:由已知,取一定点,M(1,1)
设N(x,y)为圆上的任意一点,0为原点。
则OM=(1,1),ON=(x,y)
所以
那么
又因为
所以
也就是
即
的最小值为8。
例3:已知,求的最小值。
解:由已知,可取一定点P(1,1)
再设,0为原点,
OP=(1,1)
所以
那么
的最小值为。
例4:已知:,求的最小值。
解:由已知,设,,O为原点。
所以
那么
可得
因为
所以
那么

而
即
的最小值。
例5:已知,
求的最小值。
解:由已知,设点M(),N(),O为原点
则
所以
因为
所以
也就是
即,的最小值为2。
以上五道例题利用了向量独特的几何性质和代数运算的完美结合,即向量的内积,把复杂的、看似无从入手的代数问题转化为向量问题,这不仅有助于培养学生数形结合的数学思维,还会激励学生的发散思维,使其在以后的解题过程中,手法更具有灵活性和技巧性。
爱华网本文地址 » http://www.aihuau.com/a/360151/112141794957.html
更多阅读
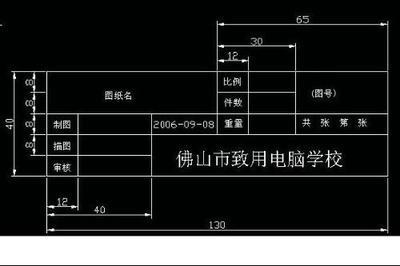
Inventor 的工程图估计是所有三维产品中对国标支持的最好的。在明细表中,我们要分别给出零件的单重和总重,同时在标题栏中还要给出所有的零件的一个总重。那么如何通过Inventor来实现这样的功能呢?首先我们将将如何在明细表中实现:1
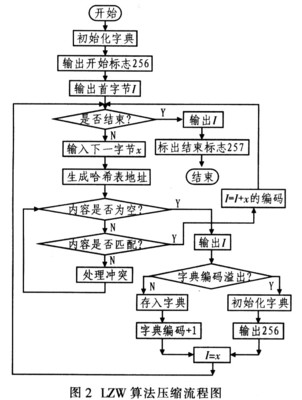
在C语言中,一个函数总是占用一段连续的内存区(位于程序的代码区),而函数名就是函数所占内存区的首地址。我们可以把函数的这个首地址(或称入口地址)赋予一个指针变量,使该指针变量指向该函数。然后通过指针变量就可以找到并调用这个函
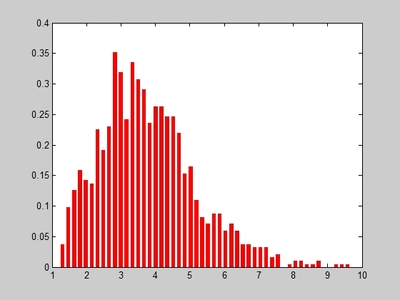
第4章概率统计本章介绍MATLAB在概率统计中的若干命令和使用格式,这些命令存放于MatlabR12ToolboxStats中。4.1随机数的产生4.1.1二项分布的随机数据的产生命令参数为N,P的二项随机数据函数binornd格式R=binornd(N,P)%N、P为二项

中国连锁加盟业发展到今天,越来越多的投资者都意识到,连锁加盟事业最大的价值在于复制成功经验、创造经济规模效益及品牌价值。这个理论固然没有错,但是,在中国市场,甚至其它亚洲市场,似乎被过度滥用,或误解为致富成功的快捷方式。

连锁加盟在台湾和大陆,甚至其它亚洲市场,似乎被过度滥用,或误解为致富成功的快捷方式。从一个单一据点或一个商业模式,要发展具备成功复制能力与价值的连锁加盟企业,并不容易;首先,创业者及这个事业,本身必须具备基本的成功要素、破坏

 爱华网
爱华网



