与T检验相比,方差分析其实就是从另一个角度看数据。
那么,它是怎么看的呢?~~且待本文分解。
从1918年费歇尔创造了方差分析,到现在快过一百岁生日了。
下图是最新一期的nature genetics,最生猛的文章,也离不开这个方差分析啊。
我们说方差分析,这个方差,实际上就是变异的意思。一词多义,至少老外的字典里是这样的。
数据的变异,大家都该了解的。我们方差分析,就是对这个方差,或者这个数据的变异进行分析。
很简单,变异可以分为哪几部分,这几部分之间什么关系?解决了这两个问题,就解决了方差分析。
试想一下,上面这组数据,分成六个亚组时,每组各自的变异情况是什么样的?把六组数据合到一起,变异情况又是什么样的?
有了上一段变异的思想,我们继续来看一下变异的分解:
很简单,把变异分为组内变异和组间变异两部分即可。下图中以数据点为例,展示了何为组内变异和组间变异:
A、B分别代表的内容理解了之后,我们看一下其在下图中的对比。
直观来看(先做一个假定),左图各组样本均数不相同,而右图则较为一致。那我们再看下其两类变异:左图中组间差异很大,右图中组间差异很小(B)。相对来说,左图中组内差异较小,而右图中组内差异较大(A)。
这说明了什么问题呢?
可不可以看出来,
如果组间差异(B)远大于组内差异(A),就意味着各组样本均数不一致呢?
是的,方差分析就是基于这样的思路:
以组内差异(A)为参考基准,考察组间差异(B)的大小。
如果组间差异(B)远大于组内差异(A),则认为组间存在区别。
而组内差异,我们认为是因为(完全)随机而产生的。以这样一个完全随机的尺度作为标杆,也甚是巧妙。
上图重新对组内、组间差异(A、B)进行了定义(上文中的A、B实际上并不是严格意义上的方差变异)。
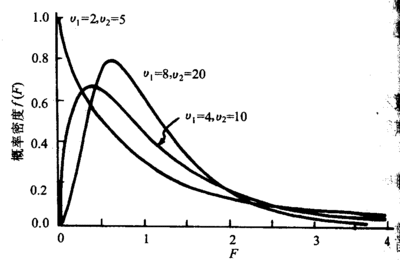
同时,我们也引出了F值,即B比A的值。
基于F分布,就很容易看出,当组间差异越大(横坐标越向右),越容易进入我们拒绝原假设(H0,各组均数相同)的区域。
一般教材上习惯这样定义方差分析的基本思想:
你理解了吗?
本文撰写匆忙,就到这里了,有疑问欢迎留言提出。
 爱华网
爱华网