用变换几何方法,巧解几何问题
初中阶段的变换几何方法主要包括对称、平移、旋转。变换几何方法是认识图形,探索图形特性的重要方法,是解决复杂问题的有效途径。我们不但要引导学生用变换几何的方法观察图形,还要善于引导学生用变换几何的方法构造图形,巧妙解决问题。举例说明如下:
一、巧用对称,构造全等
如图已知△ABC是等腰直角三角形,∠BAC=90°,AB=AC,BD是
∠ABC的平分线,CE⊥BD于点E,请判别线段BD与CE的量的关系,并证明你的结论成立。
解析:通过条件BD是∠ABC的平分线,且CE⊥BD,想到可能在∠ABC的平分线的两侧构造全等三角形,而要判别线段BD与CE的量的关系,通过观察猜想BD=2CE,于是考虑延长线段CE叫BA的延长线与点F,容易证明△BEF≌△AEC,CF=2CE,只需证明BD=CF即可。
小结:遇到角平分线或者线段垂直平分线时,并且证明结论中的线段是角平分线或者线段垂直平分线一旁的三角形的一条边时,通常在另一旁构造此三角形的全等三角形。
二、巧用平移,化零为整
求不规则图形面积时,如果各部分比较分散,通常考虑运用平移将分散图形变成一个整体。
例2.如图公园内一个矩形场地的长为60米,宽为40米,在场地内有一条对边为平行折线的甬路,甬路两侧绿化,已知EH的长为5米,求绿化区域的面积。
解析:因为甬路的对边平行,若将左侧绿化区域向右平移5米(或将右侧绿化区域向左平移5米)绿化区域恰为长为55米、宽为40米的矩形。
小结:(1)分散图形的面积之和常常通过几何变换将分散图形集中为一个图形,进行整体求解;
(2)解决平行线间的问题时常考虑将与结论有关的图形平移。
三、巧用旋转,集中条件(或结论)
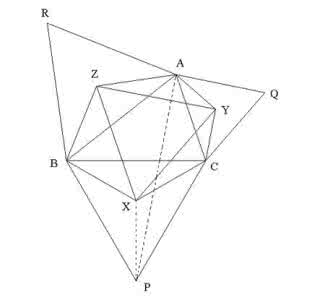
例3、如图E是正方形ABCD的边BC上的一点,AF平分∠EAD交CD于点F。
求证:AE=BE+DF。
解析:解此题的关键是如何把分散的三条线段集中到一个三角形中,经观察可通过旋转三角形达到目的。
将△ADF绕点B顺时针旋转90°到△ABG,由旋转性质可知:
△ADF≌△ABG。
则DF=BG,
∴BE+DF=BE+GB=GE
∴在△AGE中,AE=GE
∴AE=BE+DF
小结:(1)当条件或结论中的线段或角分散时,通常通过几何变换将其集中,问题便迎刃而解。
(2)在等线段较多的图形中常考虑旋转,如等腰直角三角形、等边三角形或者正方形。
 爱华网
爱华网