一. 教学内容:
具体函数应用
二. 重点、难点:
1. 一次函数()
2. 二次函数()
3. 三次函数()
4. 正比例函数()
5. 反比例函数()
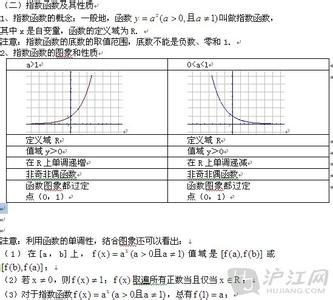
6. 指数函数(且)
7. 对数函数(且)
8. 幂函数
9. ()
10. ()
11.
【典型例题】
[例1] 已知二次函数和一次函数,其中满足,()。
(1)求证:两函数的图象交于不同的两点A、B;
(2)求线段AB在x轴上的射影A1B1的长的取值范围。
考查方向:本题主要考查考生对函数中函数与方程思想的运用能力。
知识背景:解答本题的闪光点是熟练应用方程的知识来解决问题及数与形的完美结合。
易错分析:由于此题表面上重在“形”,因而本题难点就是一些考生可能走入误区,老是想在“形”上找解问题的突破口,而忽略了“数”。
技巧方法:利用方程思想巧妙转化。
(1)证明:由消去y得
∵ ∴ ∴
∴,即两函数的图象交于不同的两点
(2)解:设方程的两根为和,则,
∵ ∴,解得
∵的对称轴方程是
时,为减函数 ∴,故
[例2] 已知关于x的二次方程
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围。
(2)若方程两根均在区间(0,1)内,求m的范围。
考查方向:本题重点考查方程的根的分布问题。
知识背景:解答本题的闪光点是熟知方程的根对于二次函数性质所具有的意义。
易错分析:用二次函数的性质对方程的根进行限制时,条件不严谨是解答本题的难点。
技巧方法:设出二次方程对应的函数,可画出相应的示意图,然后用函数性质加以限制。
解:(1)条件说明抛物线与x轴的交点分别在区间(-1,0)和(1,2)内,画出示意图,得
∴
(2)据抛物线与x轴交点落在区间(0,1)内,列不等式组
(这里是因为对称轴应在区间(0,1)内通过)
[例3] 已知对于的所有实数值,二次函数的值都是非负的,求关于x的方程的根的取值范围。
解:由条件知,即,∴
(1)当时,原方程化为
∵
∴时,时, ∴
(2)当时,
∴当时,,当时,,∴
综上所述,
[例4] 已知过原点O的一条直线与函数的图象交于A、B两点,分别过点A、B作y轴的平行线与函数的图象交于C、D两点。
(1)证明:点C、D和原点O在同一条直线上;
(2)当BC平行于x轴时,求点A的坐标。
考查方向:本题主要考查对数函数图象、对数换底公式、对数方程、指数方程等基础知识,考查学生的分析能力和运算能力。
知识背景:(1)证明三点共线的方法:。
(2)第(2)问的解答中蕴涵着方程思想,只要得到方程(1),即可求得A点坐标。
易错分析:不易考虑运用方程思想去解决实际问题。
技巧方法:本题第一问运用斜率相等去证明三点共线;第二问运用方程思想去求得点A的坐标。
(1)证明:设点A、B的横坐标分别为
由题意知:,则A、B纵坐标分别为
因为A、B在过点O的直线上,所以,点C、D坐标分别为()()
由于
所以OC的斜率:,OD的斜率:
由此可知:,即O、C、D在同一条直线上
(2)解:由BC平行于x轴知:
即,代入得
由于知,∴,又,∴,则点A的坐标为()
[例5] 在平面上有一点列,,…,,…,对每个自然数点位于函数的图象上,且点,点()与点构成一个以为顶点的等腰三角形。
(1)求点的纵坐标的表达式;
(2)若对于每个自然数,以为边长能构成一个三角形,求的取值范围;
(3)设,若取(2)中确定的范围内的最小整数,问数列前多少项的和最大?试说明理由。
考查方向:本题把平面点列,指数函数,对数、最值等知识点揉合在一起,构成一个思维难度较大的综合题目,本题主要考查考生对综合知识分析和运用的能力。
知识背景:指数函数、对数函数及数列、最值等知识。
易错分析:考生对综合知识不易驾驭,思维难度较大,找不到解题的突破口。
技巧方法:本题属于知识综合题,关键在于读题过程中对条件的思考与认识,并会运用相关的知识点去解决问题。
解:(1)由题意知: ∴
(2)∵函数递减,∴对每个自然数,有
则以为边长能构成一个三角形的充要条件是,即,解得或,∴
(3)∵,∴,∴,数列是一个递减的正数数列,对每个自然数,,于是当时,,当时,,因此数列的最大项的项数n满足不等式且
由得:,8,∴
[例6] 设是定义在R上的偶函数,其图象关于直线x=1对称,对任意,都有,且。
(1)求;(2)证明是周期函数;(3)记,求。
技巧方法:由变形为是解决问题的关键。
(1)解:因为对,都有
所以,
又因为
又 ∴ ,
(2)证明:依题意设关于直线X=1对称,故,即
又由是偶函数知,∴
将上式中以代换得,这表明是R上的周期函数,且2是它的一个周期。
(3)解:由(1)知
∵……
……
∴
又∵的一个周期是2,∴
∴,因此
[例7] 设函数的定义域为R,对任意实数x,y都有,当时,且。
(1)求证:为奇函数;
(2)在区间上,求的最值;
(1)证明:令,得令,得,
即,∴是奇函数
(2)解:任取实数且,这时
因为时,∴ ∴在上是减函数
故的最大值为,最小值为,而
∴在区间上的最大值为12,最小值为-12
[例8] 已知函数,
(1)当时,求函数的最小值;
(2)若对任意,恒成立,试求实数的取值范围。
考查方向:本题主要考查函数的最小值以及单调性问题,着重于学生的综合分析能力以及运算能力。
知识背景:本题主要通过求的最值问题来求的取值范围,体现了转化的思想与分类讨论的思想。
易错分析:考生不易考虑把求的取值范围的问题转化为函数的最值问题来解决。
技巧方法:解法一运用转化思想把转化为关于的二次不等式;解法二运用分类讨论思想解得。
(1)解:当时,
∵在区间上为增函数,∴在区间上的最小值为
(2)解法一:在区间上,恒成立恒成立
设
递增
∴当时,,当且仅当时,函数恒成立,故
解法二:
当时,函数的值恒为正;当时,函数递增,故当时,
当且仅当时,函数恒成立,故
[例9] 设是实数,记,。
(1)证明:当时,对所有实数都有意义;反之,若对所有实数都有意义,则。
(2)当时,求函数的最小值;
(3)求证:对每个,函数的最小值都不小于1。
(1)证明:先将变形,
当时,,∴恒成立,故的定义域为R
反之,若对所有实数都有意义,则只须,令,即,解得,故。
(2)解析:设
∵是增函数,∴当最小时,最小,而
显然,当时,取最小值为,此时为最小值
(3)证明:当时,
当且仅当时等号成立,∴
[例10] 已知奇函数是定义在(-3,3)上的减函数,且满足不等式
,设不等式解集为A,B=,求函数
的最大值。
考查方向:本题属于函数性质的综合性题目,考生必须具有综合运用知识分析和解决问题的能力。
知识背景:主要依据函数的性质去解决问题。
易错分析:题目不等式中的“”号如何去掉是难点,在求二次函数在给定区间上的最值问题时,学生容易漏掉定义域。
技巧方法:借助奇偶性脱去“”号,转化为的不等式,利用数形结合进行集合运算和求最值。
解:由得且,故
又∵是奇函数,∴,又在(-3,3)上是减函数
∴,即,解得或
综上得,即,
∴=
又知在B上为减函数
∴
【模拟试题】
1. 若不等式对一切恒成立,则的取值范围是( )
A. B. C. D.
2. 设二次函数,若,则的值为( )
A. 正数 B. 负数 C. 非负数 D. 正数、负数和零都有可能
3. 已知二次函数,若在区间内至少存在一个实数,使,则实数的取值范围是 。
4. 二次函数的二次项系数为正,且对任意实数恒有,若,则的取值范围是 。
5. 已知实数满足关系式(且)
(1)令,求的表达式;(2)若时,有最小值8,求和的值。
6. 如果二次函数的图象与轴的交点至少有一个在原点的右侧,试求的取值范围。
7. 二次函数中实数、、满足=0,其中,求证:
(1) (2)方程在(0,1)内恒有解。
8. 一个小服装厂生产某种风衣,月销售量(件)与售价P(元/件)之间的关系为=,生产件的成本R=元。
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
9. 函数与的图象可能是( )
10. 定义在区间(-∞,+∞)的奇函数为增函数,偶函数在区间的图象与的图象重合,设,给出下列不等式:① ;② ;③ ;
④ 其中成立的是( )
A. ①与④ B. ②与③ C. ①与③ D. ②与④
11. 若关于的方程有实根,则实数的取值范围是 。
12. 设为实数,函数,(1)讨论的奇偶性;(2)求的最小值。
13. 设。
(1)证明:在其定义域上的单调性;
(2)证明:方程有惟一解;
(3)解不等式
14. 定义在上的函数满足①对任意,都有
;② 当时,有,求证:
。
【试题答案】
1. C
解析:当即时,不等式为,恒成立,∴,当时,则满足,解得,所以的范围是。
2. A
解析:∵的对称轴为,且,则,而
∴,∴,∴。
3.
解析:只需或即或。∴
4.
解析:由知为对称轴,由于距对称轴较近的点的纵坐标较小,∴,∴
5. 解:(1)由得
由知,代入上式得
∴ ,即
(2)令,则
① 若,要使有最小值8,则在上应有最大值,但在上不存在最大值。
② 若,要使有最小值8,则应有最小值
∴ 当时, 由得,∴所求,
6. 解:∵
(1)当时,二次函数图象与轴有两个交点且分别在y轴两侧,符合题意。
(2)当时,则解得
综上所述,的取值范围是且
7. 证明:(1)
由于是二次函数,故,又,所以
(2)由题意,得
① 当时,由(1)知
若,则,又,所以在内有解
若则
又,所以在内有解
② 当时同理可证
8. 解:(1)设该厂的月获利为,依题意得
由知
∴,∴,解得
∴当月产量在件之间时,月获利不少于1300元。
(2)由(1)知
∵为正整数,∴或33时,y取得最大值为1612元。
∴当月产量为32件或33件时,可获得最大利润1612元。
9. C
解析:分类讨论当时和当时
10. C
解析:用特值法,根据题意,可设,又没
则
∴
又
∴
即①与③成立
11. 解析:设,则原方程可变为①
方程①有两个正实根,则解得:
12. 解:(1)当时,函数,此时为偶函数;当时,,此时函数既不是奇函数也不是偶函数。
(2)① 当时,函数,若,则函数在上单调递减,从而,函数在上的最小值为
若,则函数在上的最小值为,且
② 当时,函数
当时,则函数在上的最小值为:,
且,若,则函数在上单调递增
从而,函数在上的最小值为
综上,当时,函数的最小值是
当时,函数的最小值是;当时,函数的最小值是
13.(1)证明:由得的定义域为(-1,1),易判断在(-1,1)内是减函数
(2)证明:∵ ∴ ,即是方程的一个解
若方程还有另一个解,则
由反函数的定义知,与已知矛盾,故方程有惟一解
(3)解:,即
∴或
14. 证明:对中的,令,得
再令,又得,即
∴ 在上是奇函数
设,则
∵ ∴ ∴
于是由②知,从而,即
故在上是单调递减函数
根据奇函数的图象关于原点对称,知在上仍是递减函数,且
∵
∴
∵时,有,∴,故原结论成立
 爱华网
爱华网