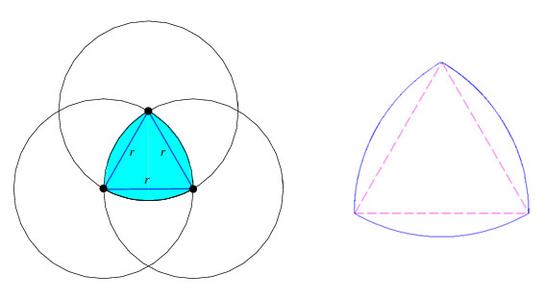
通过勒贝格积分可以算出,勒洛三角是定宽曲线所能构成的面积最小的图形,其面积为1/2[π-(3^1/2)]s^2,s为定宽宽度。
1、莱洛三角形也是“除了圆形以外,还有什么形状的下水道盖不会掉入下水道?”这个问题的一个答案。
2、下图为此类三角形旋转的一个例子,因为这个特点,该类三角形可用于做运输的轮子,搬东西稳定。
3、莱诺三角形形状的钻头可钻出正方形的孔。
井盖为什么是圆的?
合理答案之一:圆形是等宽曲线,掉不下去,安全。
这个“合理”答案其实是错的。——首先,问题是错的,有方形的井盖,虽然少见,但的确存在。
等宽曲线有无穷多种,都“掉不下去”,所以,“圆形”只是安全的充分条件,而非必要条件。
等宽曲线,通俗点说,就是用游标卡尺无论从哪个角度量,量出来的宽度都相同。同一宽度的等宽曲线,面积最大的圆,最小的是 Reuleaux 三角形 (鲁列斯三角形/莱洛三角形)。
莱洛三角形的一大用途是 Wankel 转子发动机。相比常见的活塞往复式发动机,转子发动机震动小、转速高、结构简单。鬼子产的马自达汽车上就用了 Wankel 转子发动机。关于 Wankel 转子发动机,曾在泡泡网上看到过一篇内容很详尽的贴子。莱洛三角形的另一用途是做能凿出方眼儿的钻头。
按:或许很多人以能提出/答对这些古怪的题目而骄傲不已,但是从更高的地方往下一看,其实非常滑稽。故,最可怕的是不知道自己不知道,凡事还是三缄其口好。
 爱华网
爱华网