空间几何体
二、教学目标:
1、认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实世界中简单物体的结构,了解柱、锥、台、球的概念。
2、了解画立体图形三视图的原理,并能画出简单几何图形(长方体、球、圆柱、圆锥、棱柱等简易组合)的三视图。能识别上述三视图所表示的立体模型,会用斜二测法画出立体图形的直观图。
3、掌握棱柱、棱锥、棱台、圆柱、圆锥、圆台的表面积及体积计算公式,能直观感知空间几何体的展开图的形状,并能初步运用于实际问题之中。
三、知识要点
(一)棱柱、棱锥、棱台
1、棱柱的性质:
棱柱的两个底面是全等的多边形,且对应边互相平行,侧面都是平行四边形.
2、棱锥的特点:底面是多边形,各侧面是有一个公共顶点的三角形。
3、棱台:
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台。
(1)侧面是梯形.
(2)两底是相似多边形.
(二)圆柱、圆锥、圆台
将矩形、直角三角形、直角梯形分别绕着它的一边、一直角边、垂直于底边的腰所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台。这条线叫做轴,垂直于轴的边旋转而成的圆面叫做底面,不垂直于轴的边旋转而成的曲面叫做侧面,无论旋转到什么位置这条边都叫做母线。
圆柱的特点:
(1)两底互相平行且相等,平行底的截面是与底相等的圆.
(2)所有的母线都相等且平行,并与底垂直.
(3)通过轴的截面是以底为直径和母线为邻边的矩形(叫做圆柱的轴截面).
圆锥的特点:
(1)所有母线都相等.
(2)通过轴的截面是以母线为腰、底圆直径为底的等腰三角形(叫做圆锥的轴截面).
圆台的特点:
通过轴的截面是以上、下底直径为底、母线为腰的等腰梯形.
4、球
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体.
(三)重要概念:三视图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
大小:长对正,高平齐,宽相等
(四)斜二测画法
水平放置图形斜二测画法规则:
(1)在已知图形中取互相垂直的x轴、y轴.画直观图时,把它画成对应的x′轴、y′轴,使∠x′O′y′=45°(或135°).它们确定的平面表示水平平面.
(2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′轴或y′轴的线段.
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y轴的线段,长度为原来的一半.”
(五)表面积公式
1、S直棱柱侧=ch其中c为棱柱的底面周长,h为直棱柱的高。
2、S正棱锥侧=ch′(其中c为棱锥底面周长,h’为侧面等腰三角形底边上的高--斜高)
3、S正棱台侧=(c + c′)h′
4、
5、
6、
(六)体积公式
【典型例题】
例1、选择题
(1)如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A、 B、 C、 D、
(2)半径为R的半圆卷成一个圆锥,则它的体积为( )
A、 B、 C、 D、
(3)一个棱柱是正四棱柱的条件是
A、底面是正方形,有两个侧面是矩形
B、底面是正方形,有两个侧面垂直于底面
C、底面是菱形,且有一个顶点处的三条棱两两垂直
D、每个侧面都是全等矩形的四棱柱
(4)有一个几何体的三视图如下图所示,这个几何体应是一个
A、棱台 B、棱锥 C、棱柱 D、都不对
答案:(1)A (2)A (3)D (4)A
例2、填空题
(1)已知棱台的上下底面面积分别为4,16,高为3,则该棱台的体积为___________。
(2)一个棱柱至少有 个面,面数最少的一个棱锥有 个顶点,顶点最少的一个棱台有__________条侧棱。
(3)正方体ABCD-A1B1C1D1 中,O是上底面ABCD中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________。
(4)等体积的球和正方体,它们的表面积的大小关系是________。
(5)图(1)为长方体积木块堆成的几何体的三视图,此几何体共由________块木块堆成;图(2)中的三视图表示的实物为____________。
答案:(1)28 (2)5、4、3 (3)
(4)< (5)4 圆锥
例3、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长。
解:设圆台的母线长为,则
圆台的上底面面积为
圆台的下底面面积为
所以圆台的底面面积为
又圆台的侧面积
于是7πl=29π
即为所求
例4、一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积与的函数关系式,并求出函数的定义域。
解:如图,设所截等腰三角形的底边边长为.
在Rt△EOF中,
,
所以,
于是
依题意函数的定义域为
例5、已知两个几何体的三视图如下,试求它们的表面积和体积。单位:cm。
解:(1)图(1)中的几何体可看成是一个底面为直角梯形的直棱柱。直角梯形的上底为1,下底为2,高为1;棱柱的高为1。可求得直角梯形的四条边的长度为1,1,2,。
所以此几何体的体积
(2)由图可知此正三棱柱的高为2,底面正三角形的高为,可求得底面边长为4。
所以
【模拟试题】
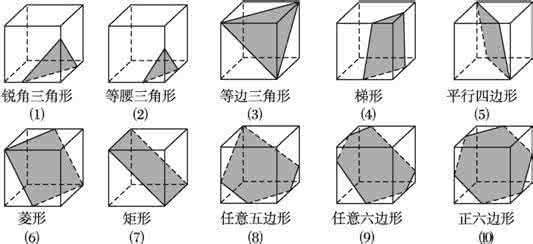
1、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去8个三棱锥后,剩下的几何体的体积是( )
A、 B、 C、 D、
2、长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是
A、 B、 C、 D、都不对
3、正方体的内切球和外接球的半径之比为( )
A、 B、 C、D、
4、如图,在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使其绕直线BC旋转一周,则所形成的几何体的体积是
A、 B、 C、 D、
5、如图,E、F分别为正方体的面、面的中心,则四边形在该正方体的面上的射影可能是___________。
6、圆台的较小底面半径为1,母线长为2,一条母线和底面的一条半径有交点且成60度角,则圆台的侧面积为 。
7、中,,将三角形绕直角边旋转一周所成的几何体的体积为_____________。
8、一个正四棱台形状的油槽,可以装油,假如它的两底面边长分别等于和,求它的深度为多少?
9、养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12m,高4m。养路处拟建一个更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变)。
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
【试题答案】
1、D 2、B 3、D 4、D
5、②③ 6、6 7、
8、解:由题意有
∴
9、解:(1)如果按方案一,仓库的底面直径变成16m,则仓库的体积
如果按方案二,仓库的高变成8m,则仓库的体积
(2)如果按方案一,仓库的底面直径变成16M,半径为8M.
棱锥的母线长为
则仓库的表面积
如果按方案二,仓库的高变成8M.
棱锥的母线长为
则仓库的表面积
(3)
 爱华网
爱华网