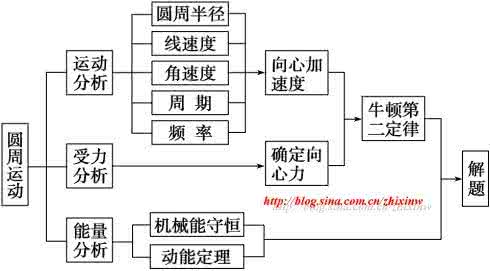
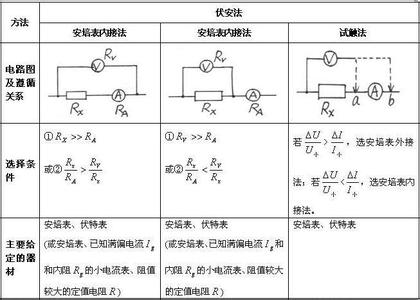
孙恒芳教你学物理-------高中物理中的数学方法——圆的妙用
方程与函数知识在高中物理中有非常广泛的应用,与之相比,几何知识的应用范围就狭窄得多,但有些物理问题能够巧妙运用几何知识便捷地解决。在高中物理课程中与几何知识结合最紧密的应该是图像问题,关于物理图像与数学图像的联系与区别,以后我们会专门讨论,接下来以“圆”为角度总结下高中物理相关知识。
高中物理知识中需用到的“圆”按其作用与功能可分为“矢量圆”“等时圆”“等势圆”“等圆系”“谐振圆”等。本文试通过几例来阐述辅助圆在解题中的妙用。
一、矢量圆
矢量即有大小,又有方向,且运算时满足平行四边行法则。在矢量的合成与分解中若能借助“矢量圆 ”就能有效地化繁为简,并能加深对矢量概念的理解。在力度分解与运动的合成与分解处常会用到。
二、等时圆
等时圆模型
如图所示,竖直放置的圆环,若物体从最高点沿各光滑弦下滑至轨道与圆弧的交点,或圆弧上任意一点沿各光滑弦下滑至最低点,其下滑的时间相等.这样的圆环称之为“等时圆”。在解决有关动力学问题时,恰当地构建等时圆不但能化解难点,而且能激发学生的解题思维。
四、等圆系
带电粒子进入匀强磁场,若带电粒子的速度大小、方向不定,则粒子在磁场中作一系列圆心、半径在时刻变化的“等圆系”,构建等圆系能化俗为奇。
五、谐振圆
当一个质点在一平面上做匀速圆周运动时,它的投影点的运动是简谐运动,这个圆通常称为“谐振圆”。换个说法,匀速圆周运动可以分解为两个相互正交的简谐运动。利用谐振圆,可以把振动这部分知识融为一体,而且它利用学生相对熟悉的圆周运动为起点,降低了学生的认知难度。利用谐振圆,能使问题直观明了,在求解振动的时间问题时尤显优势。
利用“圆”解高中物理问题时有其独特的魅力,不仅能使抽象的物理问题更形象、直观,求解过程简洁明了,而且还具有创新意识,对提高解题能力和发展求异思维无疑有很大的帮助。
 爱华网
爱华网