第14计 鲜花开门 情有独钟
●计名释义
冬天的梅花,非常耀眼.其实,梅花开的并不艳丽,只是因为你喜欢她,所以才心明眼亮.如果到了百花盛开的春天,你能身在花丛眼不花,还能看到淡淡素素的梅花吗?
数学解题也经常遇到这种情景,有时已知条件非常之多,提供的信息诱惑也非常之泛.此时,你能“情有独钟”地筛选出你需要的她吗?
●典例示范
【例1】 P点在平面内作匀速直线运动,
速度向量v=(4,-3).(P点沿v方向运动,每秒
移动的距离是|v|).开始时P(-10,10),
求5秒后P点的位置.
【分析】 本质是对P点运动的速度向量
v=(4,3)的理解:因为P点按匀速直线
运动,每秒位移是5.从速度分解观点看,
每秒P向右移4,向下移3.
【解答】 5秒P向右移20,下移15,
设P点5秒后到P′(x, y).
x=-10+20=10,y=10-15=-5. 所以P′(10,-5). 例1题图
【点评】 这样解题很轻松,善于抓住数学本质的理性思维习惯是在学习数学的过程中累积形成的,而不是在“题海战术”式的“强化训练”、“大练兵”中形成的.
【插语】 如果不按上述方式,而是从寻找=5v=(20,-15), 再求=+
当然也能求出结果,但是并不省时间.众所周知,高考中的时间就是分数.
【例2】 (04·全国Ⅰ卷)函数y=+1(x≥1)的反函数是 ( )
A.y=x2-2x+2 (x<1) B.y=x2-2x+2(x≥1)
C.y=x2-2x(x<1) D.y=x2-2x(x≥1)
【解答】 本题的鲜花是利用互反函数的性质.原函数x≥1时,y≥1.∴反函数的定义域为x≥1,排除A、C.∵点(5,3)在f (x)的图象上,∴点(3,5)必在f -1(x)的图象上,而点(3,5)适合B,不适合D,∴选B.
【点评】 与反函数有关的选择题,要注意利用其“定义域与值域互易,对应法则互逆,图象关于直线y=x对称”等特点,前呼后拥.
【例3】 下列各式中,最小值为2的是 ( )
A. B. C. D.
【思考】 利用均值不等式“取等”的条件这朵鲜花去开门.用均值不等式求最值必须满足两个条件:(1)参与运算的量必须是正数;(2)只有当有关量可以“取等”时才有最值.∵
故故否定A;当a,b异号时,否定C;当sinx<0时,亦有<0,否定D; ∴选B.
【点评】 可用直接法证明,∵存在且在分母中出现,∴ab>0.又a+b+2=(a+1)+(b+1)≥2,∴≥2. 当且仅当a=b=1时
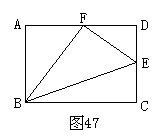
【例4】 已知四边形ABCD
为矩形且AB≠BC, PA⊥平面ABCD, 连接
AC,BD,PB,PC,PD,则以下各组向量中,数量
积不为零的是 ( )
A. B.
C. D. 例4题图
【思考】 利用图形的特点这朵花来打开解题之门.互相垂直的两向量,其数量积为零.
同理,C. ∵PA⊥平面ABCD, ∴,排除D,选A.
【点评】 可用反证法证明不垂直, 假定.∵PA⊥平面ABCD, ∴, 四边形ABCD是正方形, 这与题设AB≠BC矛盾.
●对应训练
1.若f (x)sinx是周期为π的偶函数,则f (x)可以是①sinx, ②cosx, ③cotx, ④tan中的 ( )
A.①② B.①④ C.③④ D.①
2.下列五个命题:①|a|=a2; ②; ③(a·b)2=a2·b2; ④(a- b)2=a2-2ab+b2;⑤若a·b=0,则a=0或b=0.其中正确命题的序号是 ( )
A.①②③ B.①④ C.①③④ D.②⑤
3.已知等比数列{an}的公比为q,下列命题正确的是 ( )
A.若q>1, 则{an}为递增数列 B.若0<q<1,则{an}为递减数列

C.若q<1, 则{an}为无穷递减等比数列 D.以上都不对
●参考答案
1.D【思考】 利用选项的结构特点. 选项中有三项含①,故先检验①.
设F(x)= f (x)sinx, 如果f (x)=sinx,则F(x)=sin2x=(1-cos2x).
∵cos2x(从而F(x))是周期为π的偶函数,∴f (x)可以是①,否定C(无须检验③),如果f (x)= cosx,则F(x)=sinxcosx=sin2x是周期为π的奇函数,与要求不符,否定A;如果f (x)=tan=,则F(x)=1-cosx是周期为2π的偶函数,也与要求不符, 否定B.于是f (x)仅可以是①, 选D.
【点评】 排除法解选择题也要讲求效率,设法使工作量减到最少.
2.B利用向量运算的性质. ∵a与b共线,其夹角为0.∴a2=a·a=|a||a|cos0=|a|2.①正确排除D;设a, b夹角为θ. 则而向量运算中不含除法运算,,②不能成立,排除A;若a⊥b,且a≠ b,则(a·b)2=0而a2·b2≠0, ∴③不能成立,排除C.
3.D选用特殊值取. q=2>1时,a1=-1<0, 则{an}为递减数列,排除A;当0<q=<1时,若a1=-1<0,则{an}为递增数列,排除B;取q=-2<1, a1=1,则{an}为摆动等比数列,排除C.
 爱华网
爱华网