波利亚在《怎样解题》这本书中说,我们在寻找解题方法时,可以试试在题目上做些变化,比如类比、特殊化、普遍化、分解和重组等。
我们就来说说,怎么用分解和重组的方法来解题。
例题:甲乙丙丁四车同时在一条路上行驶,甲车12点追上丙车,14点与丁相遇,16点与乙相遇,乙车17点与丙相遇,18点追上丁。问:丙和丁几点几分相遇?
这是一道行程问题,但是常规题目里该有的的路程、速度和时间,这道题里都没有,条件却很多。如果我们上来就设个x、y,闷着头开始计算,很容易失去方向。我们应该从分解条件开始。
图形是一种很好的工具,能够帮助我们分析。但现在,我们可能只能画出这样一张草图:
这张草图里能看出一些最基本的信息:甲、丙两车同方向行驶,甲车比丙车快;而乙、丁两车向另一个方向行驶,乙车比丁车快。
但也仅此而已。题目里大量关于时间的条件,都还没用上。
要用上这些信息,一种好方法是用自己的语言重新叙述,只要其中的干货。比如,具体的时间点没什么用,应该把它们换成时间段。这样,甲12点追上丙,14点遇见丁就可以理解成:甲追上丙后,再过2个小时和丁相遇。
题目没有告诉我们这四辆车是几点,从什么位置出发的。我们可以把12点当作各车出发的时间,此时甲车和丙车正好在同一个地点,对面开来乙车和丁车,乙车的位置要远一些:
甲14点与丁相遇,此时甲、丁各开了2个小时:
再过2个小时,甲与乙相遇,此时甲、乙各开了4个小时,那么甲开的距离应等于与丁相遇时的两倍。
同样的,乙车17点与丙车相遇,各开了五个小时:
乙车18点追上丁车,各开了6个小时:
然后,我们把分解了的信息组合起来, 画一张更加精准的图。这张图不需要百分之百的精确,但至少不能犯一些会导致误解的错误,像表示甲车行驶了4小时的线段,不能比表示甲车行驶2小时的线段更短:
这道行程的应用题,已经变成了一道算线段长度的题目。
现在,我们可以引入符号了。
我们用甲来表示甲车一小时的行程,也就是红线的一格,乙、丙、丁以此类推。甲和丁之间的距离用a来表示,甲和乙之间的距离用b来表示。
我们把上面的条件分别写成代数式:
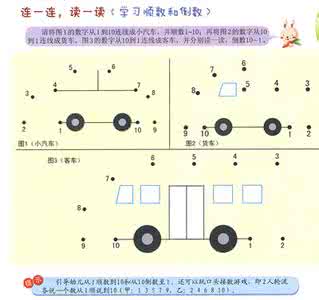
2甲+2丁=a
4甲+4乙=b
5丙+5乙=b
6乙-6丁=b-a
要算的是a÷(丙+丁)。
开始计算之前,再快速检查一下:我们用到了所有的条件了吗?如果用到了,我们就可以更加放心大胆的去算。
计算的结果等于10/3,即15点20分。
分解和组合是一种基本的分析方法。这样的数学题目,可以多做一些。
介绍其他解题方法的往期文章请看:
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网!
 爱华网
爱华网