数学开放题是相对于传统的封闭题而言的一种题型。由于客观世界复杂多变,数学问题也必然复杂多变,往往不可能得到唯一答案。
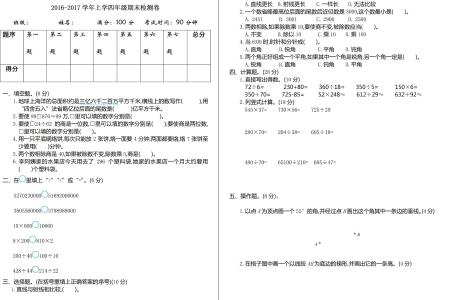
一般而言,数学开放题具有以下三个特征:
1,条件不足或多余;
2,没有确定的结论或结论不唯一;
3,解题的策略、思路多种多样。
解答数学开放题,需要我们从不同角度分析和思考问题,紧密联系实际,具体问题具体分析。我们一般可以从以下几方面考虑:
1,以问题为指向,对现有条件进行筛选、补充和组合,促进问题的顺利解决;
2,根据知识之间的不同联系途径对给定的条件进行不同的组合,采用不同的方法求解;
3,避免“答案唯一”的僵化思维模式,联系实际考虑可能出现的多种情况,得出不同的答案。
例1:A、B都是自然数,且A+B=10,那么A×B的积可能是多少?其中最大的值是多少?
分析与解答: 由条件“A、B都是自然数,且A+B=10”,可知A的取值范围是0 ~ 10,B的取值范围的10 ~ 0。不妨将符合题意的情形一一列举出来:
0×10=0 1×9=9 2×8=16 3×7=21 4×6=24 5×5=25
A×B的积可能是0、9、16、21、24、25。当A=B=5时,A×B的积的最大值是25。
从以上过程发现,当两个数的和一定时,两个数的差越小,积越大。
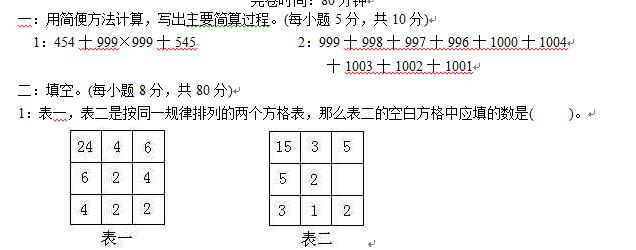
例2:把1 ~ 5五个数分别填 图中的五个圆圈内,使每条直线上三个圆圈内各数的和是9。
分析与解答:
每条直线上三个圆圈内各数的和是9,两条直线上数的和等于9×2=18(其中中间圈内的数重复加了一次)。而1、2、3、4、5的和为15,18-15=3。所以,中间圈内应填3。这样,两条直线上的圆圈中可以分别填1、3、5与2、3、4。
这个解我们也叫做基本解,由这个基本解很容易得出其余的七个解。
例3:把1 ~ 6六个数分别填入图中的六个圆圈中,使每条边上三个数的和都等于9。
分析与解答:
每边上三个数的和都等于9,三条边上数的和等于9×3=27,27-(1+2+3+4+5+6)=6。所以,三个顶点处被重复加了一次的三个数的和为6。在1 ~ 6,只有1+2+3=6,故三个顶点只能填1、2、3。这样就得到一组解:1、5、3;1、6、2;3、4、2。
例4:在一次羽毛球比赛中,8名运动员进行淘汰赛,最后决出冠军。共打了多少场比赛?(两名运动员之间比赛一次称为一场)
分析与解答: 8名运动员进行淘汰赛,第一轮赛4场后,剩下4名运动员;第二轮赛2场后,剩下2名运动员;第三轮只需再赛1场,就能决出冠军。所以,共打了4+2+1=7场球。
还可以这样想:8名运动员进行淘汰赛,每淘汰1名运动员,需要进行1场比赛,整个比赛共需要淘汰8-1=7名运动员,所以共打了7场比赛。
例5:
一个学生从家到学校,如果以每分钟50米的速度行走,就要迟到8分钟;如果以每分钟60米的速度前进,就可以提前5分钟到校。这个学生出发时离上学时间有多少分?
分析与解答: 解答这道题,可以以不同的时间为标准,选择的标准不同,解答方法也有所不同。例如,如果直接以这个学生出发时离上学的时间为标准。可这样分析:由“每分钟行50米,要迟到8分钟”,可知学校上课时,这个学生还离学校50×8=400米;由“每分钟行60米,可以提前5分钟到校”,可知距学校上课时,他还可走60×5=300米。两种不同的速度,在相同的时间内路程相差400+300=700米,而两种速度每分钟相差60-50=10米。因此,这个学生出发时离上课时间为:700÷10=70分钟。
解法一:(50×8+60×5)÷(60-50)=70分;
解法二:60×(5+8)÷(60-50)-8=70分;
解法三:50×(8+5)÷(60-50)+5=70分。
 爱华网
爱华网