相关解答一:高中数学知识点总结
一、集合与简易逻辑1.集合的元素具有确定性、无序性和互异性.2.对集合 , 时,必须注意到“极端”情况: 或 ;求集合的子集时是否注意到 是任何集合的子集、 是任何非空集合的真子集.3.对于含有 个元素的有限集合 ,其子集、真子集、非空子集、非空真子集的个数依次为 4.“交的补等于补的并,即 ”;“并的补等于补的交,即 ”.5.判断命题的真假 关键是“抓住关联字词”;注意:“不‘或’即‘且’,不‘且’即‘或’”.6.“或命题”的真假特点是“一真即真,要假全假”;“且命题”的真假特点是“一假即假,要真全真”;“非命题”的真假特点是“一真一假”.7.四种命题中“‘逆’者‘交换’也”、“‘否’者‘否定’也”.原命题等价于逆否命题,但原命题与逆命题、否命题都不等价.反证法分为三步:假设、推矛、得果.注意:命题的否定是“命题的非命题,也就是‘条件不变,仅否定结论’所得命题”,但否命题是“既否定原命题的条件作为条件,又否定原命题的结论作为结论的所得命题” .8.充要条件二、函 数1.指数式、对数式2.(1)映射是“‘全部射出’加‘一箭一雕’”;映射中第一个集合 中的元素必有像,但第二个集合 中的元素不一定有原像( 中元素的像有且仅有下一个,但 中元素的原像可能没有,也可任意个);函数是“非空数集上的映射”,其中“值域是映射中像集 的子集”.(2)函数图像与 轴垂线至多一个公共点,但与 轴垂线的公共点可能没有,也可任意个.(3)函数图像一定是坐标系中的曲线,但坐标系中的曲线不一定能成为函数图像.3.单调性和奇偶性(1)奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同.偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.注意:(1)确定函数的奇偶性,务必先判定函数定义域是否关于原点对称.确定函数奇偶性的常用方法有:定义法、图像法等等.对于偶函数而言有: .(2)若奇函数定义域中有0,则必有 .即 的定义域时, 是 为奇函数的必要非充分条件.(3)确定函数的单调性或单调区间,在解答题中常用:定义法(取值、作差、鉴定)、导数法;在选择、填空题中还有:数形结合法(图像法)、特殊值法等等.(4)既奇又偶函数有无穷多个( ,定义域是关于原点对称的任意一个数集).(7)复合函数的单调性特点是:“同性得增,增必同性;异性得减,减必异性”.复合函数的奇偶性特点是:“内偶则偶,内奇同外”.复合函数要考虑定义域的变化。(即复合有意义)4.对称性与周期性(以下结论要消化吸收,不可强记)(1)函数 与函数 的图像关于直线 ( 轴)对称.推广一:如果函数 对于一切 ,都有 成立,那么 的图像关于直线 (由“ 和的一半 确定”)对称.推广二:函数 , 的图像关于直线 (由 确定)对称.(2)函数 与函数 的图像关于直线 ( 轴)对称.(3)函数 与函数 的图像关于坐标原点中心对称.推广:曲线 关于直线 的对称曲线是 ;曲线 关于直线 的对称曲线是 .(5)类比“三角函数图像”得:若 图像有两条对称轴 ,则 必是周期函数,且一周期为 .如果 是R上的周期函数,且一个周期为 ,那么 .特别:若 恒成立,则 .若 恒成立,则 .若 恒成立,则 .三、数 列1.数列的通项、数列项的项数,递推公式与递推数列,数列的通项与数列的前 项和公式的关系: (必要时请分类讨论).注意: 2.等差数列 中:(1)等差数列公差的取值与等差数列的单调性.(2) 两等差数列对应项和(差)组成的新数列仍成等差数列.(3) 仍成等差数列.(4“首正”的递减等差数列中,前 项和的最大值是所有......余下全文>>
相关解答二:如何构建高中数学知识体系?
数学不好提高成绩,就是因为内容多,题多,所以构建知识体系相当重要。怎么办呢?
第一,熟悉课本知识。到什么程度算是熟悉了呢?就是翻开目录,能说出每一章节内容,概念,公式,定理,重要例题。这是结果。到底怎么办怎么做?没好法儿,只有一条就是多看书。开始时,一节课看一章,越来越熟悉,后来就能一节课看一本书。因为熟悉的东西不用细看了,所以就快了。要永远记住的一条就是,记忆永远是学习的最重要环节和过程,不论什么方法不都是为了记住吗?只有记住了,才谈到理解。不要说记不住,没有记不住的东西。想一想,乘法口诀怎么那么熟练呢,因为当时你下的功夫多呀。
第二,课本掌握后,先是分散开来的知识,现在要综合起来,串起来。用什么串?那根金线是什么?在哪里?那金线是“一题多解”,用题解把不同内容联系起来。比如,证明三点共线,你有几种办法?可以用向量,可用距离,可以用斜率,可以用直线方程等等,往下就想,每种办法里面,是有什么什么条件才行的?到这,就考察你的第一步课本知识掌握的好与差了。
第三,高中数学,就是集合、向量做为工具,来研究函数和几何,你就这样简单想就行了。在战略上蔑视敌人。
第四,“闻过则喜”,做错的题对你来说比做对了更有益处。做错题,一定要弄明白哪里错了,原因是什么,写出准确的原因,写在题的边上。不要每次简单地写上“马虎”“公式没记清”等词句,这样词多了,你就得又回第一步去了。
第五,学会放弃,两不做。承认有不会做的题。老师也有不会的,要老师全会,他当年也不至于考师范院校了。太难的题,不做;太巧的题,不做。
第六,厚脸皮。不会就问,不论别人说什么,只要你不懂,你就问,哪怕很简单,要脸皮厚一点。当然,问问题也要有技巧,不要问概念问公式这类课本上有的只是你没记住的东西,要问的是题,具体的题目,当然是你做了以后才问,别老师问你这题已知什么求什么都不清楚就问,那样不仅没面子还会自己觉得白痴。有问题尽量问老师,有老师就问老师,别等老师走了问同桌,老师讲题一定比同学讲的好讲的多。还有就是,别老师在教室转了好几圈你也没事,他刚到办公室你就屁颠似的追去了。长点眼睛,别在他黒着脸生气时还不知趣就行了。哈哈,说的远了点。
第七,当读完题,你能记住题意,想到是什么内容,相关公式定理一下子就从脑海里闪现出来了,在这部份做错过多少题(当然不是要你想起个数来)跌过多少跟头,被老师白眼过几次,说明你差不多了。比如,立体几何题,读完题,脑子里要有图,边、角、及各种关系都清楚,当然具体数据可不用记住,但哪个是已知总得记住吧。
第八,第七条说是差不多了,那怎么才成功了完完全全好呢,只要你不上大学,在高中永远不行。这就是所谓“只缘身在此山中”。
吹了半天牛,关键还在于你是否用功了。用句名言吧:在科学上没有平坦的大道,只有不畏劳苦,沿着陡峭山路攀登的人,才有希望达到光辉的顶点。
相关解答三:高中数学知识与大学有联系吗
学理科的也不用担心的,其实关系也不是太大
上过高中你一定知道高中知识与初中有多大关联吧?其实差不多就那一回事。
大学数学看起来深奥,其实考的内容不会太难,都是基本的。所以上了大学只要你平时学了,考试差不多就不会挂。
如果你报考的是南方的大学,署期就多准备些防晒用品,军训是很晒很辛苦的,心理准备要做充分点。
至于基础科目,不同的专业,不同学校可能不一样,文理科之间也有差别。我是学理科的,就我知道的数学、英语、物理、计算机这四样是无论如何鸡要必修的,具体开课的时间不一定在上学期。
相关解答四:高中数学知识点总结
高中数学知识点总结
1. 对于集合,一定要抓住集合的代表元素,及元素的“确定性、互异性、无序性”。
中元素各表示什么?
注重借助于数轴和文氏图解集合问题。
空集是一切集合的子集,是一切非空集合的真子集。
3. 注意下列性质:
(3)德摩根定律:
4. 你会用补集思想解决问题吗?(排除法、间接法)
的取值范围。
6. 命题的四种形式及其相互关系是什么?
(互为逆否关系的命题是等价命题。)
原命题与逆否命题同真、同假;逆命题与否命题同真同假。
7. 对映射的概念了解吗?映射f:A→B,是否注意到A中元素的任意性和B中与之对应元素的唯一性,哪几种对应能构成映射?
(一对一,多对一,允许B中有元素无原象。)
8. 函数的三要素是什么?如何比较两个函数是否相同?
(定义域、对应法则、值域)
9. 求函数的定义域有哪些常见类型?
10. 如何求复合函数的定义域?
义域是_____________。
11. 求一个函数的解析式或一个函数的反函数时,注明函数的定义域了吗?
12. 反函数存在的条件是什么?

(一一对应函数)
求反函数的步骤掌握了吗?
(①反解x;②互换x、y;③注明定义域)
13. 反函数的性质有哪些?
①互为反函数的图象关于直线y=x对称;
②保存了原来函数的单调性、奇函数性;
14. 如何用定义证明函数的单调性?
(取值、作差、判正负)
如何判断复合函数的单调性?
∴……)
15. 如何利用导数判断函数的单调性?
值是( )
A. 0B. 1C. 2D. 3
∴a的最大值为3)
16. 函数f(x)具有奇偶性的必要(非充分)条件是什么?
(f(x)定义域关于原点对称)
注意如下结论:
(1)在公共定义域内:两个奇函数的乘积是偶函数;两个偶函数的乘积是偶函数;一个偶函数与奇函数的乘积是奇函数。
17. 你熟悉周期函数的定义吗?
函数,T是一个周期。)
如:
18. 你掌握常用的图象变换了吗?
注意如下“翻折”变换:
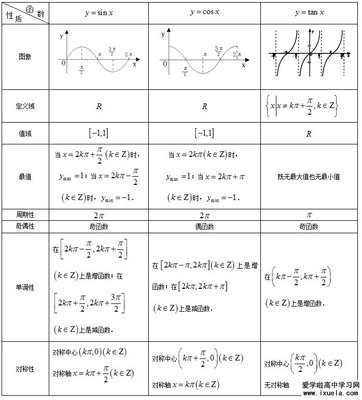
19. 你熟练掌握常用函数的图象和性质了吗?
的双曲线。
应用:①“三个二次”(二次函数、二次方程、二次不等式)的关系——二次方程
②求闭区间[m,n]上的最值。
③求区间定(动),对称轴动(定)的最值问题。
④一元二次方程根的分布问题。
由图象记性质! (注意底数的限定!)
利用它的单调性求最值与利用均值不等式求最值的区别是什么?
20. 你在基本运算上常出现错误吗?
21. 如何解抽象函数问题?
(赋值法、结构变换法)
22. 掌握求函数值域的常用方法了吗?
(二次函数法(配方法),反函数法,换元法,均值定理法,判别式法,利用函数单调性法,导数法等。)
如求下列函数的最值:
23. 你记得弧度的定义吗?能写出圆心角为α,半径为R的弧长公式和扇形面积公式吗?
24. 熟记三角函数的定义,单位圆中三角函数线的定义
25. 你能迅速画出正弦、余弦、正切函数的图象吗?并由图象写出单调区间、对称点、对称轴吗?
(x,y)作图象。
27. 在三角函数中求一个角时要注意两个方面——先求出某一个三角函数值,再判定角的范围。
28. 在解含有正、余弦函数的问题时,你注......余下全文>>
相关解答五:高中数学知识点总结 60分
不知道你是哪里高考, 地方数学文科理科都差别大的多。我按我们这里广东给你讲,理科。
大题题型有三角函数,概率,空间几何,数列,函数应用,圆锥曲线 这6个模块。
1三角函数。
▲主要熟记三角函数各种变换公式,简单的是sin(π+x) cos(π+x) tan(π+x)这一类, 还有sin(a+b)=sinacosb+sinbcosa sin(a-b)=sinacosb-sinbcosa cos(a+b)=cosacosb-sinasinb cos(a-b)同之前,但是中间是加号。 这4个公式我是这样记的, sin(a+b)是等式前后同号,sin扣扣sin, cos(a+b)是等式前后异号,扣扣sinsin。 cos2a=cos^2-sin^2 还有cos^2+sin^2=1 这个公式有时需要应用。 如1/cos^2a-tan^2a=0 可以化简成 cos^2a+sin^a/cos^a-tan^a=0 接下来是sin^2a=1-cos2a/2 cos^a=1+cos2a/2 这2个只需要记下符号很简单。 还有容易在三角函数题型里考到的就是基本不等式,a+b》2√ab 两数相加就能用。
▲图像
T=2π/w 图像移动是左加右减,上加下减。确立函数时要化成中括号形式 sin[w(x+b)]b就是直接移动的数值, bw才是函数直观看到的那个值。 还有找零点时,设方程wx+wb=0或π 需要移动就是wx+wb-wz=0或π,同样cos就是π/2这个点。
纯粹个人手打, 我也是今年高考。 加分继续补充其他模块。 不懂情追问
相关解答六:高中数学知识大全好用还是高中数学知识清单好用?急!!!
对于文科生来说高中数学知识清单比较好用
相关解答七:高中数学知识结构框架图
1.集合、简易逻辑
理解集合、子集、补集、交集、并集的概念;
了解空集和全集的意义;
了解属于、包含、相等关系的意义;
掌握有关的术语和符号,并会用它们正确表示一些简单的集合。
理解逻辑联结词"或"、"且"、"非"的含义;
理解四种命题及其相互关系;掌握充要条件的意义。
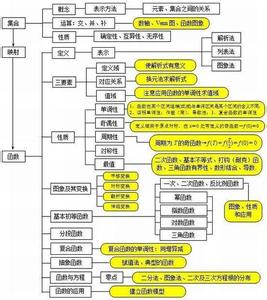
2.函数
了解映射的概念,在此基础上加深对函数概念的理解。
了解函数的单调性的概念,掌握判断一些简单函数的单调性的方法。
了解反函数的概念及互为反函数的函数图象间的关系,会求一些简单函数的反函数。
理解分数指数的概念,掌握有理指数幂的运算性质;掌握指数函数的概念、图象和性质。
理解对数的概念,掌握对数的运算性质;掌握对数函数的概念、图象和性质。
能够运用函数的性质、指数函数、对数函数的性质解决某些简单的实际问题。
3.不等式
理解不等式的性质及其证明。
掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用。
掌握分析法、综合法、比较法证明简单的不等式。
掌握二次不等式,简单的绝对值不等式和简单的分式不等式的解法。
理解不等式:|a|-|b|≤|a+b|≤|a|+|b|。
4.三角函数(46课时)
理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算。
掌握任意角的正弦、余弦、正切的定义,
并会利用单位圆中的三角函数线表示正弦、余弦和正切。
了解任意角的余切、正割、余割的定义;
掌握同角三角函数的基本关系式:
掌握正弦、余弦的诱导公式。
掌握两角和与两角差的正弦、余弦、正切公式;
掌握二倍角的正弦、余弦、正切公式;通过公式的推导,了解它们的内在联系,从而培养逻辑推理能力。
能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明(包括引出积化和差、和差化积、半角公式,但不要求记忆)。
了解周期函数与最小正周期的意义;
了解奇偶函数的意义;并通过它们的图象理解正弦函数、余弦函数、正切函数的性质;以及简化这些函数图象的绘制过程;
会用"五点法"画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A、ω、φ的物理意义。
会由已知三角函数值求角,并会用符号 arcsin x、arccos x、arctan x表示。
掌握正弦定理、余弦定理,并能运用它们解斜三角形,能利用计算器解决解斜三角形的计算问题。
5.平面向量
理解向量的概念,掌握向量的几何表示,
了解共线向量的概念。
掌握向量的加法与减法。
掌握实数与向量的积,理解两个向量共线的充要条件。
了解平面向量的基本定理,
理解平面向量的坐标的概念,
掌握平面向量的坐标运算。
掌握平面向量的数量积及其几何意义,
了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件。
掌握平面两点间的距离公式,
掌握线段的定比分点和中点坐标公式,并且能熟练运用;
掌握平移公式。
6.数列
理解数列的概念,
了解数列通项公式的意义;
了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项。
理解等差数列的概念,
掌握等差数列的通项公式与前 n 项和公式,并能解决简单的实际问题。......余下全文>>
相关解答八:初中几何里面需要学些什么才能跟的上高中数学知识?
成人高考..攻...
我本来是一个15岁的中学生,现在读初三。很擅长数学
关于几何,你要用到的不只是四边形而已。
高中要讲圆的标准方程
当然要用到函数和圆的知识
还有高中的好多思想都和初中有密切的联系。
不是我夸张
你想学好高中的知识,必须先从初中入手。
因为无论是几何还是代数,初中的东西都是基础。
像你那样好高骛远,高中的知学着也费劲
还有,就是关于你说的有用和无用。
我认为,数学的知识没有什么有用和无用。
如果把科学分成有用和无用的话,显然你的功利心极强。
这样的功利心,是无法也不能学好一门科学的。
知识的百分之九十九都是储备的。说不定什么时候能用上。
你认为没用的东西,到了恰当的时候就有用。
就是你这样毛毛草草的学了初中数学,高中未必能学好。
即使高中能学好,大学的时候,你的弊端还是要不断显露出来的。
你即使没见过金字塔,也大概知道金字塔什么样。金字塔的底非常大,而越往高越小。
金字塔结结实实,经历了风风雨雨,依然如故。
学知识也是这样啊,就像金字塔所暗示的,必须要重视基础
这样你的知识才不会出现断层,你知识的金字塔才不会倒下。
我给你的建议:刻苦的学习,
毕竟你是一个成人。应该比孩子们强许多。
至于哪部分有用的问题,我想说的是:全都有用。
一步一个脚印,打下扎实的基础,相信你会成功的
相关解答九:高中知识清单 数学 和 高中数学知识大全 哪个好
从教师角度看:都可以,关键是取决于学生本身看不看,得吃透知识点,现在的资料都差不多,大同小异,很多都是雷同的,一本就可以,不用多买。数学是日积月累的,希望孩子好好学习,成绩进步!
相关解答十:用高中数学已学知识怎么解三次函数里的x?
亲,一般都是考的特别的~_~
用到的知识点就是平方差公式还有三次方展开式盯_~
a²-b²=(a+b)(a-b) a³-b³=(a-b)(a²+ab+b²)
做你那道题给你一些启发哦:
原式=2(x³-x²)+1-x²=2x²(x-1)-(x+1)(x-1)=(x-1)(2x²-x-1)=(x-1)(2x+1)(x-1)=(x-1)²(2x+1)
所以答案就是x=1或者x=-1/2
【考试考得不会太难,一般都是看你细不细心的,其实考的就是分解因式嘛】
祝你好运~_~
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网
 爱华网
爱华网