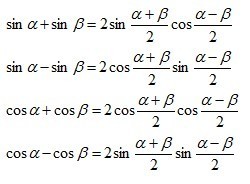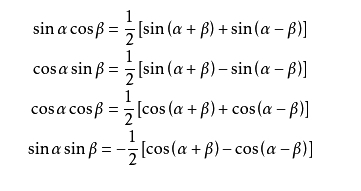两角和与差的三角函数,二倍角的正弦,余弦和正切
二. 重点、难点:
1. 掌握两角和与差的正弦、余弦、正切公式;能正确运用上述公式,进行简单三角函数的化简、求值和恒等式的证明。
2. 掌握二倍角的正弦、余弦、正切公式;能正确运用上述公式,进行简单三角函数式的化简、求值和恒等式的证明。
【典型例题】
[例1](1)已知,,其中,,求的值;(2)已知都是锐角,且,,求。
解:(1)∵
∴
∴
∴
(2)∵ ∴
又 ∵
∴
又 ∵ 在之间,余弦值为的角只有,∴
[例2] 已知锐角中,。
(1)求证:;
(2)设,求AB边上的高。
解:(1)证明:∵
∴
∴
(2)∵
∴ 即
将代入上式并整理得
解得,舍去负值,得
∴
设AB边上的高为CD
则
由AB=3,得
∴ AB边上的高等于
[例3] 已知,求的值。
解:∵ ∴
又 ∵ ∴
∴
∵
∴ 原式
[例4] 已知三点A()、B()、C()。若向量
(为常数且),求的最大值、最小值及相应的值。
解:由已知
移项得
两式平方,整理有
∴
∵
∴ 当时,有最大值
又 ∵ ,故有最小值为,此时
解得或
综上所述,当时,有最大值,当或时,有最小值。
[例5] 已知,。
(1)求及;
(2)若的最小值是,求的值。
解:(1)
(∵ )
(2)
∵ ∴
① 当时,,矛盾
② 当时,,由,得
③ 当,时,,由,得,矛盾。
综上,为所求
[例6] 设,,,与的夹角为,与的夹角为2,,求的值。
解:根据题意,
而 ∴
同理,
,而,
∴
将代入,得
∴
[例7] 如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中。
(1)将十字形的面积表示为函数;
(2)为何值时,十字形的面积最大?最大面积是多少?
解:(1)设S为十字形的面积,
则
(2)方法一:
其中
当,即时,S最大
所以当时,S最大,S的最大值为
方法二:因为
所以
令,即
可解得
所以当时,S最大,S的最大值为
【模拟试题】
一. 选择题:
1. 已知,则的取值范围是( )
A. B. C. D.
2. 的值是( )
A. B. C. D. 1
3. 要使有意义,则应有( )
A. B.
C. 或 D.
4. 等于( )
A. B. C. 1 D.
5. 已知,则等于( )
A. B. C. D.
6. 在中,若,则是( )
A. 直角三角形 B. 等边三角形
C. 钝角三角形 D. 等腰直角三角形
7. 已知,当时,可化简为( )
A. B. C. D.
8. 若,则的值是( )
A. B. C. D. 1
二. 解析题:
1. 已知,。
(1)求的值;
(2)求满足的锐角
2. 如图所示,有一块以点O为圆心的半圆形空地,要在这块空地上划出一个内接矩形ABCD辟为绿地,使其一边AD落在圆的直径上,另两点B、C落在半圆的圆周上,已知半圆的半径长为,如何选择关于点O对称的点A、D的位置,可以使矩形ABCD的面积最大?
3. 已知为锐角,且,,试求的值。
【试题答案】
一.
1. D
解析:设,两式相加得
由,得,两式相减,得,由,得 ∴
2. B
解析:原式
3. D
解析:
由
4. B
解析:
5. B
解析:
∴
∵ 在第一或第三象限,则在第一或第二象限
又 ∵
∴ 在第二象限,故
6. B
解析:由,得
又 ∴
∴ ∴
,A=B,同理B=C ∴ 是等边三角形
7. D
解:
∵
∴
∴ ,
∴ 原式
8. B
解析:
二.
1. 解析:(1)因为,所以
所以
由
所以
(2)因为
所以 所以
因为为锐角,所以
2. 解析:如图所示,令,则,则矩形ABCD的面积为
其中“”中等号成立的充要条件是,即
于是时,S为最大
不难得到,这时A、D两点与O的距离都是
3. 解析:由题意知
∵ ∴ ∴ ,
(1)÷(2),,即
又 ∵ ∴
∴ ∴ ∴
∴
 爱华网
爱华网