明代珠算家程大位在其所著《直指算法统宗》(1592年)中有这样一道题:“假如井不知深,先将绳三折入井,绳长四尺;后将绳四折入井,亦长一尺。问井深及绳长各若干?”答曰:“井深八尺,绳长三丈六尺。”
巧算绳子量井深
这星期我们学校进行了“数学之星”比赛,有一道难题把我给难住了:绳子量井深。爷爷把绳子三折以后放进井里,露在外面的绳长是4米;爷爷又把绳子四折以后放进井里,露在外面的绳长是1米。请你算一算,井有多深?绳子有多长?
我觉得这道题非常有趣,但是不知从哪儿下笔。后来我就请教了妈妈,妈妈让我根据题意先画一下草图,然后问了我几个问题,顿时让我茅塞顿开,一下子明白了。
问题1:“绳子三折以后放进井里,露在外面的绳长是4米”,实际露在外面的是几米?
这太简单了,我脱口而出:“三四十二,12米喽!”
问题2:“绳子四折以后放进井里,露在外面的绳长是1米”, 实际露在外面的又是几米?
我觉得更简单了:“4米。”
问题3:少了几米?这几米到哪里去了?
我想了想,12-4=8米,可算出这个有什么用呢?我仔细地看着自己画的草图,忽然一拍脑门,叫起来:“妈妈,我知道了,8米跑到井里去了!”原来,三折的绳子只有3段在井里,四折的绳子有4段在井里,这多出来的1段就使得井外的绳子少了8米。也就是说,井深是8米。算出了井深,算绳子的长度就轻而易举了:8×3+3×4=36米或8×4+1×4=36米。
绳子量井深,原来也不难,这道数学题太有意思了,我以后一定还要多做做。
小花狗老奶目不识丁,记性很好,旧社会女孩不能上学,在家纺花,老舅爷在家中诵读书本。老奶就背会了“百家姓”、“三字经”等,就是“鸡兔同笼”这些算术题也熟记在心。其中也常给爷爷讲一道类似的测量井深的题目。题是这样的:
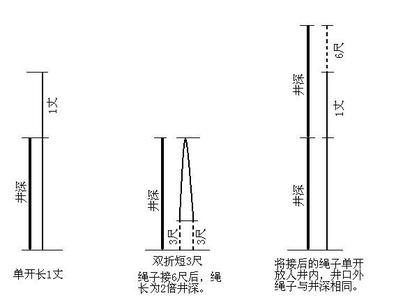
井有井恁深,绳有绳恁长,用绳量井深,单开长1丈,双起短3尺。问井有多深,绳有多长?
解题:双起短3尺,那将绳子接上2个3尺,也就是6尺正好是2倍井深。单时绳子已长了1丈,现在又接了6尺,井深就是1丈6,绳子长度就是再加1丈,2丈6了。
 爱华网
爱华网