106.证明直线与直线的垂直的思考途径
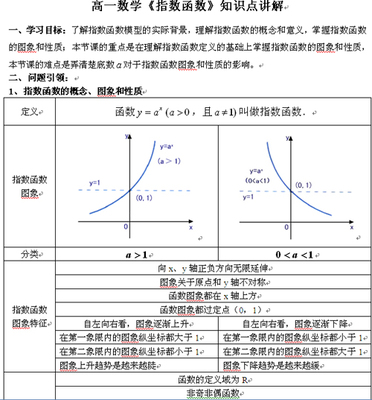
1转化为相交垂直;
2转化为线面垂直;
3转化为线与另一线的射影垂直;
4转化为线与形成射影的斜线垂直.
107.证明直线与平面垂直的思考途径
1转化为该直线与平面内任一直线垂直;
2转化为该直线与平面内相交二直线垂直;
3转化为该直线与平面的一条垂线平行;
4转化为该直线垂直于另一个平行平面。
108.证明平面与平面的垂直的思考途径
1转化为判断二面角是直二面角;
2转化为线面垂直;
(3) 转化为两平面的法向量平行。
109.空间向量的加法与数乘向量运算的运算律
(1)加法交换律:+=+.
(2)加法结合律:(+)+=+(+).
(3)数乘分配律:λ(+)=λ+λ.
110.平面向量加法的平行四边形法则向空间的推广
始点相同且不在同一个平面内的三个向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所表示的向量.
111.共线向量定理
对空间任意两个向量、 (≠ ),∥存在实数λ使=λ.
三点共线.
、共线且不共线且不共线.
112.共面向量定理
向量与两个不共线的向量、共面的存在实数对,使.
推论 空间一点P位于平面MAB内的存在有序实数对,使,
或对空间任一定点O,有序实数对,使.
113.对空间任一点和不共线的三点A、B、C,满足,则当时,对于空间任一点,总有P、A、B、C四点共面;当时,若平面ABC,则P、A、B、C四点共面;若平面ABC,则P、A、B、C四点不共面.
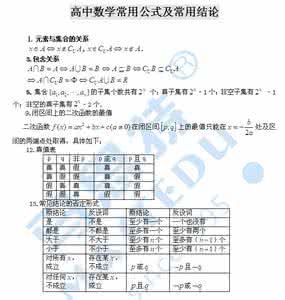
四点共面与、共面
平面ABC.
114.空间向量基本定理
如果三个向量、、不共面,那么对空间任一向量,存在一个唯一的有序实数组x,y,z,使=x+y+z.
推论 设O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的三个有序实数x,y,z,使.
115.射影公式
已知向量=和轴,是上与同方向的单位向量.作A点在上的射影,作B点在上的射影,则
116.向量的直角坐标运算
设=,=则
(1) +=;
(2) -=;
(3)λ= (λ∈R);
(4) ·=;
117.设A,B,则
= .
118.空间的线线平行或垂直
设,,则
;
.
119.夹角公式
设=,=,则.
推论 ,此即三维柯西不等式.
120. 正棱锥的侧面与底面所成的角为,则。
特别地,对于正四面体每两个面所成的角为,有。
121.异面直线所成角
=
其中为异面直线所成角,分别表示异面直线的方向向量
122.直线与平面所成角
(为平面的法向量).
123.二面角的平面角根据具体图形确定是锐角或是钝角
或,为平面,的法向量.
124折叠角定理
设AC是α内的任一条直线,AD是α的一条斜线AB在α内的射影,且BD⊥AD,垂足为D,设AB与α(AD)所成的角为, AD与AC所成的角为, AB与AC所成的角为.则.
125.空间两点间的距离公式
若A,B,则=.
126.点到直线距离
(点在直线上,为直线的方向向量, =).
127.异面直线间的距离
(是两异面直线,其公垂向量为,分别是上任一点,为间的距离).
128.点到平面的距离
为平面的法向量,,是的一条斜线段.
129.异面直线上两点距离公式
.
.
.
(两条异面直线a、b所成的角为θ,其公垂线段的长度为h.在直线a、b上分别取两点E、F,,,).
130.三个向量和的平方公式
 爱华网
爱华网