压床机构课程设计 压床机构课程设计 超好!!压床机构设计

目录

一. 设计要求----------------------------------------------------------3

1. 压床机构简介---------------------------------------------------------------3

2. 设计要求和内容-----------------------------------------------------3

二．压床机构的设计-----------------------------------------------4

1. 连杆机构的设计及运动分析---------------------------------------4

(1) 作机构运动简图并计算各杆长度-------------------------------4

(2) 机构运动速度分析-----------------------------------------------7

(3) 机构运动加速度分析---------------------------------------------8

(4) 机构动态静力分析----------------------------------------------10

三．凸轮机构设计-------------------------------------------------13

一、压床机构设计要求

1.压床机构简介

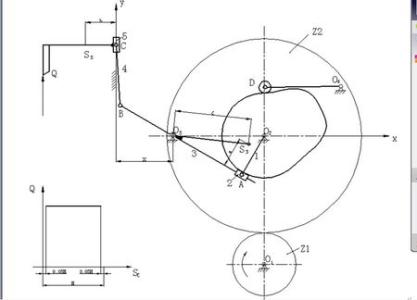
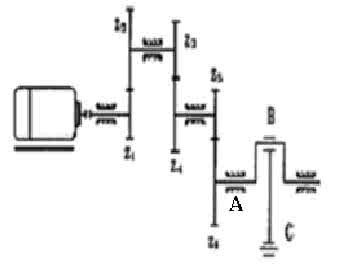
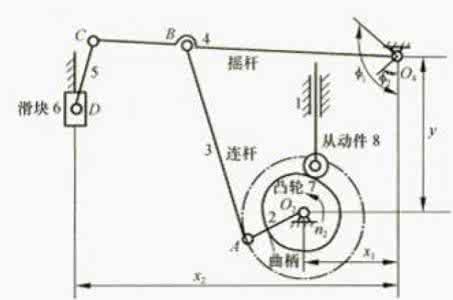
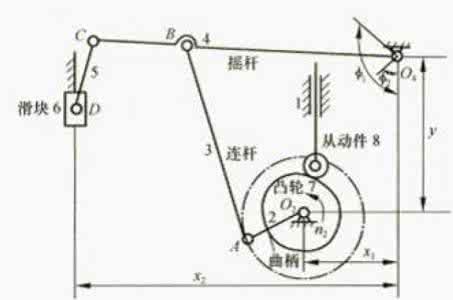
图9—6所示为压床机构简图。其中，六杆机构ABCDEF为其主体机构，电动机经联轴器带动减速器的三对齿轮z1-z2、z3-z4、z5-z6将转速降低，然后带动曲柄1转动，六杆机构使滑块5克服阻力Fr而运动。为了减小主轴的速度波动，在曲轴A上装有飞轮，在曲柄轴的另一端装有供润滑连杆机构各运动副用的油泵凸轮。

2.设计要求和内容：

（1）机构的设计及运动分折

已知：中心距x1、x2、y, 构件3的上、下极限角，滑块的冲程H，比值 CE／CD、EF／DE，各构件质心S的位置，曲柄转速n1。 要求：设计连杆机构 , 作机构运动简图、机构1～2个位置的速度多边形和加速度多边形、滑块的运动线图。以上内容与后面的动态静力分析一起画在l号图纸上。

（2）机构的动态静力分析

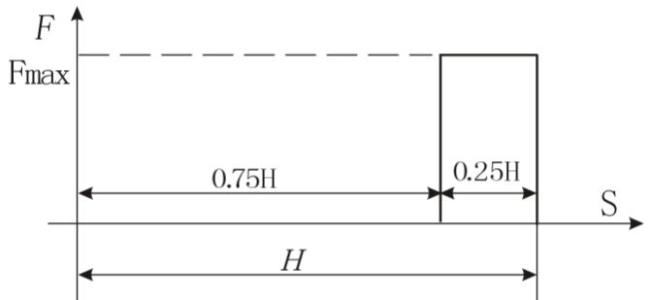
已知：各构件的重量G及其对质心轴的转动惯量Js(曲柄1和连杆4的重力和转动惯量（略去不计)，阻力线图(图2)以及连杆机构设计和运动分析中所得的结果。

要求：确定机构一个位置的各运动副中的反作用力及加于曲柄上的平衡力矩。作图部分亦画在运动分析的图样上。

（3）凸轮机构构设计

已知：从动件冲程H，许用压力角[α ]．推程角δ。，远休止角δı，回程角δ'，从动件的运动规律见表9-5，凸轮与曲柄共轴。

要求：按[α]确定凸轮机构的基本尺寸．求出理论廓

线外凸曲线的最小曲率半径ρ。选取滚子半径r，绘制凸轮实际廓线。以上内容作在3号图纸上

二、压床机构的设计

1、连杆机构的设计及运动分析 (1) 作机构运动简图并计算各杆长度

已知：Ψ3′＝60° Ψ3〞＝120°

∴∠E1DE2＝Ψ3〞-Ψ3′＝60°

过D作∠E1DE2的角平分线交E1E2于H，F1F2于I点 ∵DE1＝DE2 ∴DH⊥E1E2

∵∠HDZ＝∠HDE2+Ψ3′＝30°+60°＝90° ∴IHD是一条水平线 ∴DI⊥F1F2 ∴E1E2∥F1F2

在△E1KF1和△E2GF2中 GE2＝KF1 E2F2＝E1F1 ∠E2GF2＝∠E1KF＝90° ∴△E1KF1≌△E2GF2

∴F2G＝E1K

∵E1E2＝E1K+KE2 F1F2=F1G+GF2 ∴E1E2=F1F2=H

∵△E1DE2是等边三角形 ∴lDE1= lDE2=H=150 mm ∵EF／DE=1/4

∴lEF =1/4lDE =1/4×150=37.5 mm ∵CE/CD=1/2

∴CD=2/3DE=2/3×150=100 mm 连结AD

tanΨ=x1/y=50/220=0.225 ∴Ψ=12.7° AD=

x1

2

y

2

=

2

220=225.61 mm

2

在△ADC2和ADC1中，由余弦定理有

AC2 = AD2DC222ADDC2COS(6012.7) = 173.90

AC1 = AD2C1D22ADC1DCOS(12012.7) =272.48 ∴lAB = lBC = ∵

AC1AC2

= 49.285mm 2AC1AC2

=223.185 mm 2

DSBS211

= 3 = BCDE22

11

BC = ×223.19 =111.5925 mm 2211

DS3 = DE =×150 = 75 mm

22

∴BS2 =

（2）机构运动速度分析：

已知：n1=100r/min；

1 =

n1100

2 =10.472 逆时针 2 rad/s = 6060

v

B

= 1·lAB = 10.472×0.049285≈0.516 m/s

vC = vB + vCb 大小 ? 0.516 ?

方向 ⊥CD ⊥AB ⊥BC

选取比例尺μv=0.004（m/s）/mm，作速度多边形

v＝uv＝uv＝uv ＝uv＝u

C

v·

pc ＝0.004×18.71=0.07484m/s bc ＝0.004×121.5=0.486m/s

CBEF

v·

v·

pe ＝0.004×28.06=0.11224m/s pf

＝0.004×20.7=0.0828m/s ＝0.004×14.36=0.05744m/s

v·v·

FE

ef

vv

S2

S3

u＝u

＝

v·v·

ps2＝0.004×69.32mm ＝0.27728m/s

ps3＝0.004×14.03mm ＝0.05612m/s

vCB

∴2＝＝0.486/0.223185=2.178rad/s (顺时针)

lBC

ω3＝ω4＝

vClCDvFElEF

＝0.07484/0.1=0.7484rad/s (逆时针) ＝0.05744/0.0375=1.532rad/s (顺时针)

（3）机构运动加速度分析：

aB=ω1LAB=10.472×0.049285=5.405m/s n

aCB=ω2LBC=2.178×0.223185=1.059m/s n

aCD=ω3LCD=0.748×0.1=0.056m/s n

aFE=ω4LFE=1.532×0.0375=0.088m/s

2

2

2

2

2

2

2

2

2

2

2

2



ac= anCD+ atCD= aB + atCB + anCB

大小： ？ √ ？ √ ？ √ 方向： ？ C→D ⊥CD B→A ⊥BC C→B

选取比例尺μa=0.04(m/s2)/mm,作加速度多边形图

aC=uap'c'=0.04×113.53=4.5412m/s aE=uap'e'=0.04×170.29=6.8116m/st

aCB=uab'c'=0.04×61.3=2.452 m/s atCD=uan

2

·

2

·

2

·

2

·

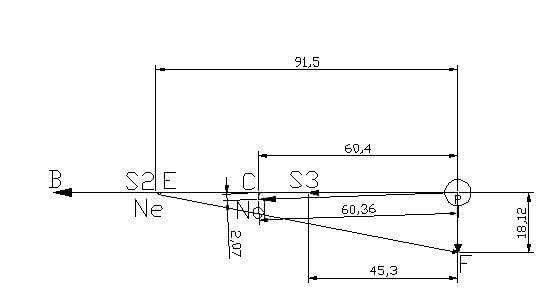
a = a + a

F

E

n

FE

+

a

t

FE

大小： √ ？ √ ? 方向： √ ↑ F→E ⊥FE

aF=uap'f'=0.04×129.42=5.1768 m/s as2=uap's2'=0.04×120.97=4.8388m/s as3=uap's3'=0.04×85.15= 3.406m/s a=uap'f'=0.04×129.42= 5.1768m/s

t

= aCB/LCB=2.452/0.223185=10.986 m/s （逆时针）

t

= aCD/LCD=4.5408/0.1=45.408 m/s （顺时针）

2

·

2

·

2

·

2

F

·

2

2

2

3

（4）机构动态静力分析

Fg2=m2*as2=G2*as2/g=660×4.839/9.8=325.892N（与as2方向相同） Fg3=m3*as3= G3*as3/g=440×3.406/9.8=152.922N（与as3方向相反） Fg5= m5*aF=G5*aF/g=300×5.177/9.8=158.480N（与aF方向相反） Fr=Frmax/10=4000/10=400N

MI2=Js2*α2=0.28×10.986=3.076N.m （顺时针） MI3=Js3*α3=0.085×45.408=3.860N.m （逆时针） hg2= MI2/Fg2=3.076/325.892=9.439mm hg3= MI3/Fg3=3.860/152.922=25.242mm

2．计算各运动副的反作用力 (1)分析构件5

对构件5进行力的分析，选取比例尺μF=10N/mm，作其受力图

构件5力平衡： Fg5+G5+R65+R45=0 则R45=-μFL45=-10×47.44=-474.4N R43=-R45=474.4N

R65=μFL65=10×12.18=121.8N

(2)分析构件2、3 单独对构件2分析：

t

杆2对C点求力矩，可得：R12*LBC -G2*LG2 -Fg2*LFg2 =0 t

R12×223.19-660×19.38-325.892×0.96=0 t

R12= 58.711N

单独对构件3分析： 杆3对C点求矩得： t

R63*LCD-G3*hG3+R43*hR43+Fg3*hFg3=0 t

R63×100-440×21.73+474.4×35.65+152.922×0.24=0

t

解得R63=265.103N

对杆组2、3进行分析：

ttnn

R43+Fg3+G3+R63+ Fg2+G2+R12+R12+R63=0 大小：√ √ √ √ √ √ √ ？ ？ 方向：√ √ √ √ √ √ √ √ √ 选取比例尺μF=10N/mm，作其受力图

nn

则 R12=10×156.8=1568N； R63=10×49.28=492.8N.

(3)求作用在曲柄AB上的平衡力矩Mb：

Mb=F21*LR21=156.91×10×0.00855=13.416 N.m

R61=R21=156.91×

10=1569.1N.

11

三、凸轮机构设计

取r0=38mm 取rr=4mm 在推程过程中：

由a=π2hω2 cos(πδ/δ0)/（2δ02）得

当δ0 =550时，且00=0,即该过程为加速推程段, 当δ0 =550时,且δ>=22.50, 则有a

在回程阶段，由a=-π2hω2 cos(πδ/δ0′)/ (2δ0′2)得

当δ0′=850时，且00=42.50, 则有a>=0,即该过程为加速回程段 所以运动方程S=h[1+cos(πδ/δ0′)]/2 12

凸轮廓线如下:

参考文献：

1. 陆风仪主编．机械原理课程设计．北京．机械工业出版社.2002 2. 孙 恒、陈作模、葛文杰主编．机械原理．北京．高等教育出版社．2006

13

14

爱华网本文地址 » http://www.aihuau.com/a/372951/507831324333.html