导读
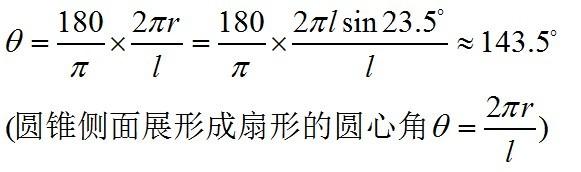
数学英才“三角形内角和等于180°”,这对于我们来说是再熟悉不过的一个常识,陈省身教授从一个不同的角度去看待这个问题,并将这个问题延伸推广,于1944年,找到了一般曲面上封闭曲线方向改变量总和的公式(高斯—比内—陈公式),把几何学引入了新的天地,被誉为划时代的贡献。
美籍华人陈省身教授是当代举世闻名的数学 家,他十分关心祖国数学科学的发展。人们称 赞他是“中国青年数学学子的总教练”。
1980年,陈教授在北京大学的一次讲学中语惊四座:
“人们常说,三角形内角和等于180°。但是,这是不对的!”
大家愕然。怎么回事?三角形内角和是180°,这不是数学常识吗?
接着,这位老教授对大家的疑问作了精辟的解答:
说“三角形内角和为180°”不对,不是说这个事实不对,而是说这种看问题的方法不对,应当 说“三角形外角和是360°”!
把眼光盯住内角,只能看到:
三角形内角和是180°;
四边形内角和是360°;
五边形内角和是 540°;
…………
n边形内角和是(n-2)×180°。
这 就找到了一个计算内角和的公式。公式里出现 了边数n。
如果看外角呢?
三角形的外角和是360°;
四边形的外角和是360°;
五边形的外角和是360°;
…………
任意n边形外角和都是360°。
这就把多种情形用一个十分简单的结论概况起 来了。用一个与n无关的常数代替了与n有关的 公式,找到了更一般的规律。
设想一只蚂蚁在多边形的边界上绕圈子(图1)。每经过一个顶点,它前进的方向就要改变一次,改变的角度恰好是这个顶点处的外角。爬了一圈,回到原处,方向和出发时一致了,角度改变量之和当然恰好是360°。
图7
早在2000多年前,欧几里德时代,人们就已经知道三角形内角和是180°。到了19世纪,德国数学家、被称为“数学之王”的高斯,在对大地测量的研究中,找到了球面上由大圆弧构成的三角形内角和的公式。又经过几代数学家的努力,直到1944年,陈省身教授找到了一般曲面上封闭曲线方向改变量总和的公式(高斯—比内—陈公式),把几何学引入了新的天地。由此发展出来的“陈氏类”理论,被誉为划时代的贡献, 在理论物理学上有重要的应用。
从普通的、众所周知的事实出发,步步深入、推广,挖掘出广泛适用的深刻规律。从这里显示出数学家透彻、犀利的目光,也表现了数学家穷追不舍、孜孜以求的探索真理的精神。
本文选自张景中,《数学家的眼光》第一篇,中 国少年儿童出版社,原标题:三角形内角和
 爱华网
爱华网