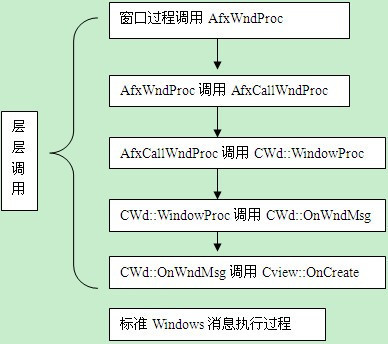
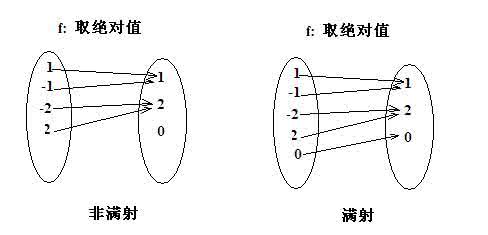
映射;函数
二. 本周教学重、难点:
1. 了解映射的概念,理解函数的概念。
2. 了解构成函数的要素,会求一些简单函数的定义域,在实际情境中,会根据不同的需要选择恰当的方法表示函数。
3. 理解函数值域的概念,掌握函数值域的几种求解方法。
【典型例题】
[例1] 设,,
(1)从M到N的映射的个数为 ;
(2)从M到N的映射满足,这样的映射的个数为 。
解:
(1)由分步计数原理和映射的概念,知这样的映射有个。
(2)若,则或;
若,则 若,则
故共有4个不同映射
[例2] 函数,若,则的所有可能值为( )
A. 1 B. C. D. 1,
解:,即
当时, ∴
当时,
∴ ∴ 只能取0,此时
∵ ∴
[例3] 规定为不超过的最大整数,例如,对实数,令,,进一步令
(1)若,分别求和;
(2)若同时满足,求的取值范围。
解析:
(1)当时, ∴ ,且
(2)由=1,得
于是 ∴
解得
[例4] 求函数的定义域
解析:由,得
借助于数轴,得函数的定义域为
[例5] 求下列函数的定义域
(1)已知的定义域为,求的定义域
解:∵ 的定义域为 ∴ ∴
∴ 的定义域为
(2)已知的定义域为[3,5],求的定义域
解:∵ 的定义域为[3,5] ∴
∴ 的定义域为
(3)已知的定义域为,求的定义域
解:∵ 的定义域为 ∴
∴ ∴ 的定义域为 ∴
∴ 由(1)知或
由(2)知或 ∴ 或
∴ 的定义域为
[例6] 求下列函数的值域;
(1);
(2);
(3);
(4)
解:
(1)方法一: ∵ ∴
∴ ,即
方法二:由 得
∵ ∴ ,解得
(2)方法一:设,得
∴
∴
方法二:∵ ∴ ∴ 定义域为
∵ 函数在上均单调递增
∴ ∴
(3)方法一:当时,,当且仅当时,取等号;
当时,=,当且仅当时,取等号
综上,所求函数的值域为
方法二:先证此函数的单调性
任取且
∵
∴ 当或时,递增
当或时,递减
故时,
时,
∴ 所求函数的值域为
(4)方法一:利用函数的有界性
将原函数化为
令且
∴
平方得 ∴
∴ 原函数的值域为
方法二:数形结合法或图象法
原函数式可化为
此式可以看作点(2,0)和()连线的斜率,而点()的轨迹方程为,如图所示,在坐标系中作出圆和点(2,0)
由图可看出,当过(2,0)的直线与圆相切时,斜率分别取得最大值和最小值,由直线与圆的位置关系知识可设直线方程为,即
易得
∴ 原函数的值域为
[例7] 已知椭圆C:(),、是椭圆的左、右焦点,A为椭圆的右顶点,的最大值的取值范围是,其中,P为椭圆上任意一点,求椭圆的离心率的取值范围。
解:设P 点坐标为
由题意知 故①
又P点在椭圆上
∴ ∴
代入①式得
又 ∵ ∴
即的最大值为
又,解得
[例8] 已知函数的图象与轴分别相交于点A、B,(分别是与轴正半轴同方向的单位向量),函数
(1)求的值;
(2)当满足时,求函数的最小值。
解:
(1)由已知得,B(0,)
则 于是 ∴
(2)由得
即 解之,得
由于,则,其中等号当且仅当,即时成立
∴ 的最小值是
【模拟试题】
一. 选择题:
1. 设集合A={1,2,3},集合B={},那么从集合A到集合B的一一映射的个数共有( )
A. 3 B. 6 C. 9 D. 18
2. 设集合A=R,集合B=正实数集,则从集合A到集合B的映射只可能是( )
A. :
B. :
C. :
D. :
3. 已知函数的定义域为R,则实数的取值范围是( )
A. B. C. D.
4. 已知,则的解析式是( )
A. B. C. D.
5. 若,则等于( )
A. B. 1 C. 3 D.
6. 函数的值域为R,则的取值范围是( )
A. B. C. D.
7. 已知实数满足,则的最小值是( )
A. B. 6 C. D. 18
8. 已知,则其反函数的定义域为( )
A. B. C. D.
二. 解析题:
1. 某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元。
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为个,零件的实际出厂单价为P元,写出函数的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
2. 函数是定义域为R的偶函数,且对任意的,均有成立。当时,
(1)当时,求的表达式;
(2)若的最大值为,解关于的不等式
3. 已知,函数
(1)当时,求使成立的的集合;
(2)求函数在区间[1,2]上的最小值。
4. 已知是正常数,
(1)求证:,并指出等号成立的条件;
(2)利用(1)的结论求函数,的最小值,并指出取最小值时的值。
【试题答案】
一.
1. B
解析:由一一映射的定义知,共有个。
2. C
解析:由题意知:对A、B选项中,若,则,对选项D中,故选C。
3. B
解析:排除法,时,定义域为R,排除A、D;时,,定义域为,不为R,排除C。
4. C
解析:设,则 ∴
∴
5. C
解析:∵ ∴
∴
6. C
解析:的值域为R,即的值域,故的最小值,即
7. D
解析:数形结合知表示原点与直线上任意一点距离的平方,故其最小值为。
8. C
解析:由互为反函数的性质,知的定义域即为的值域,由指数函数的单调性易知的值域为
二.
1. 解析:(1)设一次订购量为个时,零件的实际出厂单价恰降为51元。
由题意,得,得。
故当一次订购550个时,零件实际出厂单价恰为51元。
(2)由题意知,当时,
当时,
当时, ∴ 函数的表达式是
(3)由(2)知当销售商一次订购500个零件和1000个零件时销售单价分别为元和51元,故其利润分别是元和
元。
2. 解析:
(1)当时,
当时,,
当时,,
故当时,的表达式为
(2)∵ 是以2为周期的周期函数,且为偶函数
∴ 的最大值就是当时的最大值
∵ ∴ 在[0,1]上是减函数
∴ ∴
当时,由,得或
得
∵ 是以2为周期的周期函数
∴ 的解集为
3. 方法点拨:去绝对值号,将化为基本初等函数后,再求解。
解析:
(1)由题意
当时,
∴ 或;当时,
∴ 综上,所求解集为
(2)设此最小值为
① 当时,在区间上,
∵ ,
则是区间[1,2]上的增函数 ∴
② 当时,在区间上,
由,知
③ 当时,在区间上,
;若时,在区间(1,2)内
从而为区间[1,2]上的增函数 ∴
若时,则 当时,
∴ 在上函数递增 当时,
∴ 在上函数递减 因此当时,或
当时,,故
当时,,故
综上所述,所求函数的最小值
4. 解析:
(1)证明:应用二元均值不等式,得
故
当且仅当,即时上式取等号
(2)由(1)
当且仅当,即时上式取最小值,即
 爱华网
爱华网