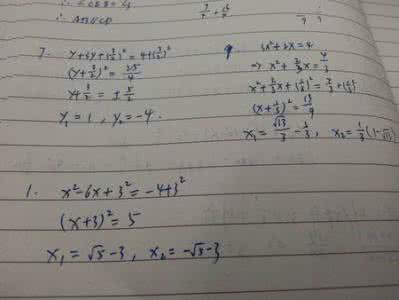
文档类型:上传人:芝兰玉树2015下载许可:是下载次数:1大小:748.5K所需奉献值:2
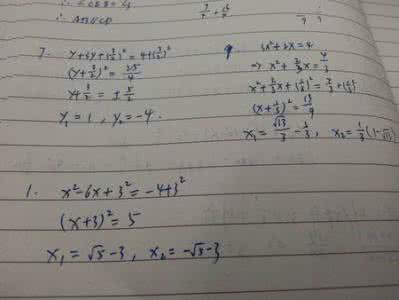

各位老师:大家好!今天我上课的内容是数学八年级(下册)第七章一元二次方程《配方法》(第二课时).下面我根据我上课的思路,从教学目标的确定、教学重点与教学难点的分析、教学方式与手段的选择、教学过程的设计四方面对本节课的教学作一个

一、学情分析:本节是在学生已经掌握了配方法解一元二次方程的基础上,从问题入手,推导求根公式,并能用公式法解简单系数的一元二次方程二、教学目标:1、使学生经历探索求根公式的过程,培养学生抽象思维能力。2、使学生熟练地应用求根公
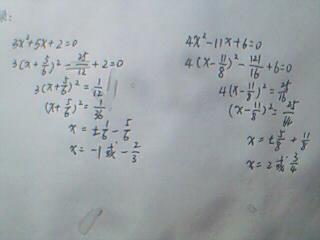
《用配方法解一元二次方程》,是本章解法的第三课时,我的设计思路如下:首先因为学生在开始已经学习了用直接开平方法和因式分解法解一元二次方程,因此通过大屏幕展示学生比较感兴趣的篱笆问题引入,从而引出本节课的内容,在学生掌握的过程

设计思想:孔子的“温故而知新”;奥苏泊尔的“先行组织者”思想;建构主义思想。设计思路:温故知新,做好铺垫;难点提前突破,水到渠成;错例分析,变式练习,加深理解,实现能力的提高。整体上,引导学生自我建构自己的知识结构。教学难点:主要等

《用配方法证明》证明书用配方法证明设矩形长为x,那么宽为15-x面积S=x(15-x)=-x^2+15x=-(x-7.5)^2+56.25≤56.25所以面积最大为56.25平方米,无法达到60平方米x-12x+40=x-12x+36+4 =(x-6)^2+4因为(X-6)^2≥0所以(X-6)^2+4≥4所以大