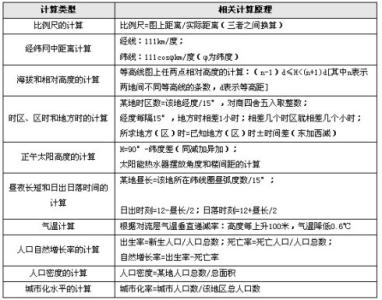
2014高考数学“拿分题”训练:函数与方程的思想方法
一、知识整合
函数与方程是两个不同的概念,但它们之间有着密切的联系,方程f(x)=0的解就是函数y=f(x)的图像与x轴的交点的横坐标,函数y=f(x)也可以看作二元方程f(x)-y=0通过方程进行研究。
就中学数学而言,函数思想在解题中的应用主要表现在两个方面:一是借助有关初等函数的性质,解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题:二是在问题的研究中,通过建立函数关系式或构造中间函数,把所研究的问题转化为讨论函数的有关性质,达到化难为易,化繁为简的目的.许多有关方程的问题可以用函数的方法解决,反之,许多函数问题也可以用方程的方法来解决。函数与方程的思想是中学数学的基本思想,也是历年高考的重点。
1.函数的思想,是用运动和变化的观点,分析和研究数学中的数量关系,建立函数关系或构造函数,运用函数的图像和性质去分析问题、转化问题,从而使问题获得解决。函数思想是对函数概念的本质认识,用于指导解题就是善于利用函数知识或函数观点观察、分析和解决问题。
2.方程的思想,就是分析数学问题中变量间的等量关系,建立方程或方程组,或者构造方程,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决。方程的数学是对方程概念的本质认识,用于指导解题就是善于利用方程或方程组的观点观察处理问题。方程思想是动中求静,研究运动中的等量关系.
3.(1)函数和方程是密切相关的,对于函数y=f(x),当y=0时,就转化为方程f(x)=0,也可以把函数式y=f(x)看做二元方程y-f(x)=0。函数问题(例如求反函数,求函数的值域等)可以转化为方程问题来求解,方程问题也可以转化为函数问题来求解,如解方程f(x)=0,就是求函数y=f(x)的零点。
(2)函数与不等式也可以相互转化,对于函数y=f(x),当y>0时,就转化为不等式f(x)>0,借助于函数图像与性质解决有关问题,而研究函数的性质,也离不开解不等式。
(3) 数列的通项或前n项和是自变量为正整数的函数,用函数的观点处理数列问题十分重要。[来源:学+科+网]
(4) 函数f(x)=(n∈N*)与二项式定理是密切相关的,利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题。
(5)解析几何中的许多问题,例如直线和二次曲线的位置关系问题,需要通过解二元方程组才能解决,涉及到二次方程与二次函数的有关理论。[来源:学科网]
(6) 立体几何中有关线段、角、面积、体积的计算,经常需要运用布列方程或建立函数表达式的方法加以解决。
二、例题解析
Ⅰ.运用函数与方程、表达式相互转化的观点解决函数、方程、表达式问题。
例1 已知,(a、b、c∈R),则有( )
(A) (B) (C) (D)
解析 法一:依题设有 a·5-b·+c=0
∴是实系数一元二次方程的一个实根;
∴△=≥0 ∴ 故选(B)
法二:去分母,移项,两边平方得:
≥10ac+2·5a·c=20ac[来源:Z.xx.k.Com][来源:Zxxk.Com]
∴ 故选(B)
点评解法一通过简单转化,敏锐地抓住了数与式的特点,运用方程的思想使问题得到解决;解法二转化为b2是a、c的函数,运用重要不等式,思路清晰,水到渠成。
练习1 已知关于的方程 -(2 m-8)x +-16 = 0的两个实根 、 满足 <<,则实数m的取值范围_______________。
答案:;
2 已知函数 的图象如下,则( )
(A) (B)
(C) (D)
答案:A.
3 求使不等式≤·对大于1的任意x、y恒成立的a的取值范围。Ⅱ:构造函数或方程解决有关问题:
例2 已知,t∈[,8],对于f(t)值域内的所有实数m,不等式恒成立,求x的取值范围。
解析∵t∈[,8],∴f(t)∈[,3]
原题转化为:>0恒成立,为m的一次函数(这里思维的转化很重要)
当x=2时,不等式不成立。
∴x≠2。令g(m)=,m∈[,3]
问题转化为g(m)在m∈[,3]上恒对于0,则:;
解得:x>2或x<-1
评析 首先明确本题是求x的取值范围,这里注意另一个变量m,不等式的左边恰是m的一次函数,因此依据一次函数的特性得到解决。在多个字母变量的问题中,选准“主元”往往是解题的关键。
例3为了更好的了解鲸的生活习性,某动物保护组织在受伤的鲸身上装了电子监测装置,从海洋放归点A处,如图(1)所示,把它放回大海,并沿海岸线由西向东不停地对它进行了长达40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动),然后又在观测站B处对鲸进行生活习性的详细观测,已知AB=15km,观测站B的观测半径为5km。
观测时刻
t(分钟)
跟踪观测点到放归
点的距离a(km)
鲸位于跟踪观测点正北
方向的距离b(km)
10
1
0.999
20
2
1.413
30
3
1.732
40
4
2.001
(1)据表中信息:①计算出鲸沿海岸线方向运动的速度;②试写出a、b近似地满足的关系式并
画出鲸的运动路线草图;
(2)若鲸继续以(1)-②运动的路线运动,试预测,该鲸经过多长时间(从放归时开设计时)可进入前方观测站B的观测范围?并求出可持续观测的时间及最佳观测时刻。(注:≈6.40;精确到1分钟)
解析(1)由表中的信息可知:
①鲸沿海岸线方向运动的速度为:(km/分钟)
②a、b近似地满足的关系式为:运动路线如图
(2)以A为原点,海岸线AB为x轴建立直角坐标系,设鲸所在
位置点P(x,y),由①、②得:,又B(15,0),
依题意:观测站B的观测范围是:
≤5 (y≥0) 又
∴≤25 解得:11.30≤x≤17.70
由①得:∴该鲸经过t==113分钟可进入前方观测站B的观测范围
持续时间:=64分钟
∴该鲸与B站的距离d==
当d最小时为最佳观测时刻,这时x==14.5,t=145分钟。
练习4.已知关于的方程-2= 0有实数解,求实数的取值范围。
(答案:0≤≤4-)
Ⅲ:运用函数与方程的思想解决数列问题
例4设等差数列{an}的前n项和为Sn,已知,>0,<0,
(1)求公差d的取值范围;
(2)指出、、…,中哪一个最大,并说明理由。
解析(1)由得:,
∵=>0 =<0
∴
(2)
∵d<0,是关于n 的二次函数,对称轴方程为:x=
∵<<Ahref="http://s4.sinaimg.cn/middle/001HPFVTzy6Ft6ec4lZe3&690"><<Ahref="http://photo.blog.sina.com.cn/list/blogpic.php?pid=001HPFVTzy6Ft6eofAV4d&bid=5d362ba10102egxk&uid=1563831201"target=_blank> ∴当n=6时,最大。
三、强化练习
1.展开式中的系数为____________.
2.已知方程的四个根组成一个首项为的等差数列,则( )
A 1 B C D
3.设双曲线的焦点在轴上,两条渐近线为,则该双曲线的离心率( )
A 5 B C D [来源:学.科.网Z.X.X.K]
4.已知锐角三角形ABC中,。
Ⅰ.求证;
Ⅱ.设,求AB边上的高。
5.甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为,甲、丙两台机床加工的零件都是一等品的概率为。
Ⅰ.分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
Ⅱ.从甲、乙、丙加工的零件中各取一个进行检验,求至少有一个是一等品的概率。
6.设,,曲线在点处切线的倾斜角的取值范围为,则点P到曲线对称轴距离的取值范围是( )
7.设双曲线C:与直线相交于两个不同的点A、B。
Ⅰ.求双曲线C的离心率的取值范围;
Ⅱ.设直线与轴的交点为P,且,求的值。
2014高考数学“拿分题”训练:化归与转化的思想在解题中的应用
一、知识整合
1.解决数学问题时,常遇到一些问题直接求解较为困难,通过观察、分析、类比、联想等思维过程,选择运用恰当的数学方法进行变换,将原问题转化为一个新问题(相对来说,对自己较熟悉的问题),通过新问题的求解,达到解决原问题的目的,这一思想方法我们称之为“化归与转化的思想方法”。[来源:学|科|网]
2.化归与转化思想的实质是揭示联系,实现转化。除极简单的数学问题外,每个数学问题的解决都是通过转化为已知的问题实现的。从这个意义上讲,解决数学问题就是从未知向已知转化的过程。化归与转化的思想是解决数学问题的根本思想,解题的过程实际上就是一步步转化的过程。数学中的转化比比皆是,如未知向已知转化,复杂问题向简单问题转化,新知识向旧知识的转化,命题之间的转化,数与形的转化,空间向平面的转化,高维向低维转化,多元向一元转化,高次向低次转化,超越式向代数式的转化,函数与方程的转化等,都是转化思想的体现。
3.转化有等价转化和非等价转化。等价转化前后是充要条件,所以尽可能使转化具有等价性;在不得已的情况下,进行不等价转化,应附加限制条件,以保持等价性,或对所得结论进行必要的验证。
4.化归与转化应遵循的基本原则:
(1)熟悉化原则:将陌生的问题转化为熟悉的问题,以利于我们运用熟知的知识、经验和问题来解决。[来源:Zxxk.Com]
(2)简单化原则:将复杂的问题化归为简单问题,通过对简单问题的解决,达到解决复杂问题的目的,或获得某种解题的启示和依据。(3)和谐化原则:化归问题的条件或结论,使其表现形式更符合数与形内部所表示的和谐的形式,或者转化命题,使其推演有利于运用某种数学方法或其方法符合人们的思维规律。(4)直观化原则:将比较抽象的问题转化为比较直观的问题来解决。(5)正难则反原则:当问题正面讨论遇到困难时,可考虑问题的反面,设法从问题的反面去探求,使问题获解。
二、例题分析
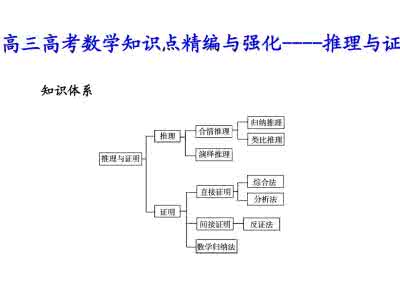
例1.某厂2001年生产利润逐月增加,且每月增加的利润相同,但由于厂方正在改造建设,元月份投入资金建设恰好与元月的利润相等,随着投入资金的逐月增加,且每月增加投入的百分率相同,到12月投入建设资金又恰好与12月的生产利润相同,问全年总利润m与全年总投入N的大小关系是( )
A. m>N B. m,且,比较与的大小。若直接求和,很难比较出其大小,但注意到等差数列的通项公式an=a1+(n-1)d是关于n的一次函数,其图象是一条直线上的一些点列。等比数列的通项公式bn=a1qn-1是关于n的指数函数,其图象是指数函数上的一些点列。
在同一坐标系中画出图象,直观地可以看出ai≥bi 则>,即m>N。[点评]把一个原本是求和的问题,退化到各项的逐一比较大小,而一次函数、指数函数的图象又是每个学生所熟悉的。在对问题的化归过程中进一步挖掘了问题的内涵,通过对问题的反思、再加工后,使问题直观、形象,使解答更清新。
例2.如果,三棱锥P—ABC中,已知PA⊥BC,PA=BC=l,PA,BC的公垂线ED=h.求证三棱锥P—ABC的体积.
分析:如视P为顶点,△ABC为底面,则无论是S△ABC以及高h都不好求.如果观察图形,换个角度看问题,创造条件去应用三棱锥体积公式,则可走出困境.[来源:学,科,网]
解:如图,连结EB,EC,由PA⊥BC,PA⊥ED,ED∩BC=E,可得PA⊥面ECD.这样,截面ECD将原三棱锥切割成两个分别以ECD为底面,以PE、AE为高的小三棱锥,而它们的底面积相等,高相加等于PE+AE=PA=l,所以
VP-ABC=VP-ECD+VA-ECD=S△ECD·AE+S△ECD·PE=S△ECD ·PA=·BC·ED·PA=.
评注:辅助截面ECD的添设使问题转化为已知问题迎刃而解.
例3.在的展开式中x的系数为( ).
(A)160 (B)240 (C)360 (D)800
分析与解:本题要求展开式中x的系数,而我们只学习过多项式乘法法则及二项展开式定理,因此,就要把对x系数的计算用上述两种思路进行转化:[来源:学科网]
思路1:直接运用多项式乘法法则和两个基本原理求解,则展开式是一个关于x的10次多项式, =(x2+3x+2)(x2+3x+2) (x2+3x+2) (x2+3x+2)(x2+3x+2),它的展开式中的一次项只能从5个括号中的一个中选取一次项3x并在其余四个括号中均选择常数项2相乘得到,故为·(3x)··24=5×3×16x=240x,所以应选(B).
思路2利用二项式定理把三项式乘幂转化为二项式定理再进行计算,∵x2+3x+2=x2+(3x+2)=(x2+2)+3x=(x2+3x)+2=(x+1)(x+2)=(1+x)(2+x),∴这条思路下又有四种不同的化归与转化方法.①如利用x2+3x+2=x2+(3x+2)转化,可以发现只有(3x+2)5中会有x项,即(3x)·24=240x,故选(B);②如利用x2+3x+2=(x2+2)+3x进行转化,则只 (x2+2)4·3x中含有x一次项,即·3x·C44·24=240x;③如利用x2+3x+2=(x2+3x)+2进行转化,就只有·(x2+3x)·24中会有x项,即240x;④如选择x2+3x+2=(1+x)(2+x)进行转化,=×展开式中的一次项x只能由(1+x)5中的一次项乘以(2+x)5展开式中的常数项加上(2+x)5展开式中的一次项乘以(1+x)5展开式中的常数项后得到,即为x·25+·24·x··15=160x+80x=240x,故选(B).[来源:学§科§网Z§X§X§K]
评注:化归与转化的意识帮我们把未知转化为已知。
例4.若不等式对一切均成立,试求实数的取值范围。解:
令,则要使它对均有,只要有
或。点评:在有几个变量的问题中,常常有一个变元处于主要地位,我们称之为主元,由于思维定势的影响,在解决这类问题时,我们总是紧紧抓住主元不放,这在很多情况下是正确的。但在某些特定条件下,此路往往不通,这时若能变更主元,转移变元在问题中的地位,就能使问题迎刃而解。本题中,若视x为主元来处理,既繁且易出错,实行主元的转化,使问题变成关于p的一次不等式,使问题实现了从高维向低维转化,解题简单易行。
三、总结提炼
1.熟练、扎实地掌握基础知识、基本技能和基本方法是转化的基础;丰富的联想、机敏细微的观察、比较、类比是实现转化的桥梁;培养训练自己自觉的化归与转化意识需要对定理、公式、法则有本质上的深刻理解和对典型习题的总结和提炼,要积极主动有意识地去发现事物之间的本质联系。“抓基础,重转化”是学好中学数学的金钥匙。
2.为了实施有效的化归,既可以变更问题的条件,也可以变更问题的结论,既可以变换问题的内部结构,又可以变换问题的外部形式,既可以从代数的角度去认识问题,又可以从几何的角度去解决问题。
 爱华网
爱华网