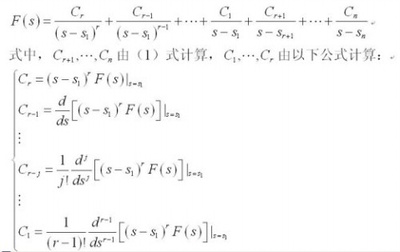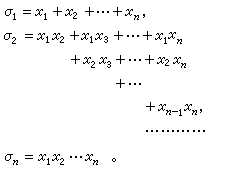几何:三角形全等判定(一)
学习目标:
代数:理解约分,会把分式化成最简分式,熟练地应用乘除法法则进行分式的乘除法运算。
几何:会用“边角边公理(SAS)”判定三角形全等。
二. 重点、难点
1. 重点:
代数:分式的乘除法运算
几何:利用“边角边公理”判定三角形全等。
2. 难点:
代数:分式乘除法法则的应用
几何:判定过程寻找条件以及按格式书写。
三. 知识要点
代数:
1.
2. 乘除法法则
几何:
2. 三角形全等判定(一):边角边公理(SAS)
有两边和它们的夹角对应相等的两个三角形全等。
怎样让角相等
怎样让边相等:图形的和差。
【典型例题】
例1. 约分
(1) (2)
(1)分析:分子、分母是多项式,先把分子、分母因式分解,找出公因式,然后约去公因式,使得分式变成最简分式,在这个分式的分母中,可把负号提到分式的前面。
解:
(2)分析:该分式的分子、分母中含有分式,可通过分式的基本性质同乘以一个数,使分子、分母变为整式。
解:
例2. 计算
分析:分式的乘除法运算属于同一级运算,应按从左往右的顺序进行计算。
解:
例3. 当时,求
分析:应先化简成最简分式,再把的值代入计算,较为方便。
解:
例4. 如图所示,AB=DC,,求证:AD//BC
分析思路:先证明△ABD≌△CDB,得,得AD//BC。
证明:在△ABD和△CDB中,
(全等三角形,对应角相等)——关键:寻找对应角
∴AD//BC(内错角相等,两直线平行)
例5. 如图所示,已知:点E是CD的中点,AD=BC,GH//DC,且,求证:AE=BE。
证明:
(两直线平行,内错角相等)
【模拟试题】(答题时间:30分钟)
一. 计算下列各式
(1)
(2)
二. 求值
(1)
(2)
(3)当的值。
三. 如图所示:AB=AD,BC=DE,,求证:
四. 如图所示,AD是的中线,E在BC的延长线上,且CE=AB,。求证:AE=2AD
【试题答案】
一. 计算下列各式
(1)
(2)
二. 求值
(1)原式
(2)原式
(3)原式=
三. 证明:
四. 证明:
 爱华网
爱华网