电学综合题历来是初中物理的难点,在近几年的中考题中屡屡出现,由于试题综合性强,设置障碍多,如果学生的学习基础不够扎实,往往会感到很难。在实际教学中,许多教师采用的是“题海战术”,无形加重了学生学习的课业负担。探索和改进电学综合问题教学,是一项很有价值的工作。
在长期的初中教学实践中,本人逐步探索了一套电学综合问题教学方案,对于学生突破电学综合问题中的障碍有一定效果。
一、理清“短路”概念。
在教材中,只给出了“整体短路”的概念,“导线不经过用电器直接跟电源两极连接的电路,叫短路。”而在电学综合题中常常会出现局部短路的问题,如果导线不经过其他用电器而将某个用电器(或某部分电路)首尾相连就形成局部短路。局部短路仅造成用电器不工作,并不损坏用电器,因此是允许的。因它富于变化成为电学问题中的一个难点。
局部短路概念抽象,学生难以理解。可用实验帮助学生突破此难点。
实验原理如图1,当开关S闭合前,两灯均亮(较暗);闭合后,L1不亮,而L2仍发光(较亮)。
为了帮助初中生理解,可将L1比作是电流需通过的“一座高山”而开关S的短路通道则比作是“山里的一条隧洞”。有了“隧洞”,电流只会“走隧洞”而不会去“爬山”。
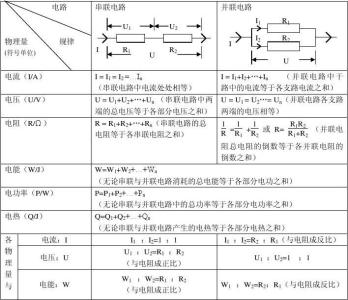
二、识别串并联电路
电路图是电学的重要内容。许多电学题一开头就有一句“如图所示的电路中”如果把电路图辨认错了,电路中的电流强度、电压、电阻等物理量的计算也随之而错,造成“全军覆没”的局面,所以分析电路是解题的基础。初中电学一般只要求串联、并联两种基本的连接,不要求混联电路。区分串、并联电路是解电学综合题的又一个需要突破的难点。
识别串、并联有三种方法,⑴、电流法;⑵、等效电路法;⑶、去表法。
⑴、电流法:即从电源正极出发,顺着电流的流向看电流的路径是否有分支,如果有,则所分的几个分支之间为并联,(分支前后有两个节点)如果电流的路径只有一条(无分支点),则各元件之间为串联。此方法学生容易接受。
⑵、等效电路法:此方法实质上运用了“电位”的概念,在初中物理中,电压的概念,是通过“水位差”的类比中引入的。那么,可借助于“高度差”进行类比,建立“一样高的电位”概念。可以通过类比手法,例如:如果某学校三层楼上有初三⑴、初三⑵、初三⑶三个班级,二层楼上有初二⑴、初二⑵、初二⑶三个班级,那么初三年级与初二年级任意两个班级之间的“高度差”是一样的,都相差“一层楼”。因为初三年级各班处于“一样高”的三层楼上,而初二年级各班级处于“一样高”的二层楼上。在电路中,也有“一样高电位”的概念。在电路中,无论导线有多长,只要其间没有用电器都可以看成是同一个点,即电位“一样高”。因此,我们可以找出各元件两端的公共点画出简化的等效电路。
图2、图3是对各电阻的连接情况分析。
图2 图3
如上图2红线上各个点都与电源正极“电位一样高”,蓝线部分与电源负极“电位一样高”,可以简化为图3。在图3中,R1、R2、R3的并联关系也就显而易见了。
⑶、去表法:由于电压表的内阻很大,并联在电路中时,通过它的电流很小,可忽略不计。故在电路中去掉电压表,不会影响电路结构,电压表所在之处可视为开路。而电流表的内阻很小,串联在电路中几乎不影响电路的电流强度,因而,在电路分析中,可视其为一根导线,去掉后改成一根导线即可。
三、“表格分析法” 整理解题思路
不少初中生反映,电学习题涉及概念、公式多,解题头绪多,容易出错。要突破这个难点,关键在于整理出清晰的解题思路。
可以使用“表格法”帮助整理解题思路。
表格的列,列出有关用电器的电流、电压、电阻、电功率四个物理量。在一般计算中,出现用电器多为纯电阻,根据欧姆定律I=U/R,电功率的计算公式P=UI,在四个物理量中只要知道了其中的两个,就可以求出剩余的两个物理量。(有六种情况)
表格的行,列出电流等物理量在各分电路和总电路的数值,或物理量在用电器的各种状态下(如额定工作状态、电路实际工作状态)的数值。而根据串、并联电路的特点或根据题设,只要知道其中的两个(或一个),就可以求出剩余的物理量。
典型例题:如图4所示,R1=2欧,R2=6欧,接在电源上时,电压表的示数为0.5伏,求电路消耗的总电功率是多少?
这是有关两个电阻串联的典型习题,
有关电阻R1的物理量:I1、U1、R1、P1;
有关电阻R2的物理量:I2、U2、R2、P2;
有关总电路的物理量:I、U、R、P。
在这12个物理量中,已知其中的三个物理量,就可以求出剩余的9个物理量。
用“表格分析法”进行解题分析如下表1
表1:
有关R1
有关R2
有关总体
横向关系
电流
I1
I2
I
电流相等
电压
U1=0.5V *
U
U=U1+U2
电阻
R1=2Ω *
R2=6Ω *
R
R=R1+R2
电功率
P1
P = ?
注:* 表示为题目中已知量。
解题分析:从表中“有关R1”的纵向可以看出,由于已知了U1和R1故可以求出I1和P1(在本题不需要求出);再由“有关电流”的横向关系来看串联电路电流处处相等,可进一步得出I2和I;再从“有关总体”的纵向来看,要求P,则除了已求出的电流I这一个物理量外,还需要在U和R两者之中知道第二个物理量,方可求出。而要求R或求U,则可以从“有关电阻”的横向关系或“有关电压”横向关系中求出来。在这一步也就可以用两种方法,所谓一题多解。
解: [有关R1纵向关系]
∵因为R1与R2串联 ∴总电流I=I1=0.25A [横向关系]
总电阻 [横向关系]
总功率 [有关总电阻纵向关系]
有一类习题,是关于灯泡的,常有额定状态和工作状态,如用“6V3W”字样已知了灯泡额定状态的电压和电功率,而工作状态则常常为“电功率最小时(或最大时)”等情况。横向关系往往在题设中出现,如设灯泡的电阻不变,或设电源的总电压不变等。
四、有关“电路变化”分析
不少同学反映“变化的电路难,不知从何下手”。这是因为分析变化的电路涉及的内容广,考虑的问题深。对电阻、电流强度、电压及电功率相互关系的分析,稍有不慎就会造成连错反应,得出错误的结论。这是电学综合问题的又一个难点。
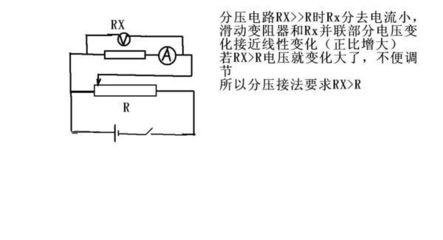
变化电路主要是通过开关或滑动变阻器的改变来富于电路变化的。电路中有多个开关,通过开关闭合和断开的状态变化,往往会使各用电器的连接关系发生变化,而滑动变阻器则通过滑片来改变其连入电路的有效电阻,从而使电路中的电压、电流、电功率等数值发生变化(也有改变电路结构的)。有关变化电路,应在学会识别“部分电路短接”和学会识别串并联电路的基础上,掌握分析变化电路的基本思路。
1、开关的通、断造成电路的变化
当开关处在不同状态时,由于断路和短路,接入电路中的用电器,及其用电器之间的连接方式一般要发生变化,因此首先要在原电路的基础上画出各种情况下的实际电路。改画时要根据电流的实际情况,运用“拆除法”。
拆除法要求:⑴、去掉被断路的元件;⑵、去掉已被短路的元件;⑶、用“去表法”去表,其原则是“电压表处是断路,电流直过电流表”。在去掉电压表时,要分析电压表读出来的是哪部分电路两端的电压,可用等效电路法进行分析。
例题:如图5所示
电路中,电源电压保持
4伏,L1的电阻为4欧,
L2、L3的电阻均为16欧
求:⑴、S1、S2都断开
时,电流表和电压表的
示数。
⑵、S1、S2都接通时,整个电路消耗的电功率。
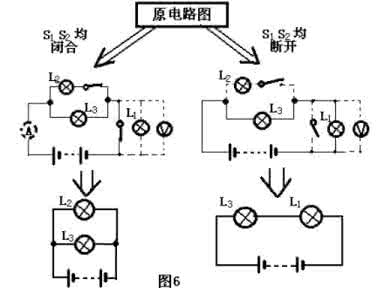
例题分析:在题中的当开关处于闭合或断开的两种情况下电路结构发生了变化,可进行电路的改画,见图6。
注:图中虚线部分是要去掉的部分。
在用“去表法”去掉电流表电压表后,要分析它们分别测量哪一个用电器的哪
一个物理量。电压表
可借助于“等电位”
进行分析。在图7中,
红线、蓝线、黑线分
别是三个“同电位点”,
由图7中可见,L1与
电压表V均加在蓝线
与黑线之间,所以电压表是L两端的电压。
解:当S1、S2都断开时,L1、L3串联。
电流表读数
电压表读数
当S1、S2都接通时,L2、L3并联。
总电阻
总功率
2.滑动变阻器变化问题
滑动变阻器连入电路中的有效电阻发生变化了,或是引起电路结构的变化,或是引起电路中电压、电流、电功率的变化。
典型例题:如图8所示电路中,电源电压不变,当滑动变阻器的滑片向右滑动时,电流表
和电压表的示数变化情况是[ ]
A、电流表和电压表的示数变大;
B、电流表和电压表的示数变小;
C、电流表示数变小,电压表示
数变大;
D、电流表示数变大,电压表示数变小。
有关滑动变阻器的此类型问题,解题关键是:⑴、弄清滑动变阻器原理,滑片滑动时电阻是变大还是变小?⑵、弄清物理量是否变化,一般来说,电源的电压,定值电阻的阻值是不变,其它的物理量都是变化的;⑶、弄清电压表读数读出的是哪一个电器两端的电压;⑷、利用表格整理分析问题的思路。
上例题表格分析如下:
有关R1
有关R2
总电路
关系
电流
I1I2
I ?
串联电流相等
电压
U1 ?
U总 不变
U总 =U1+U2
电阻
R1 不变
R2 ↑
R总
R总 =R1+R2
由电阻横向关系可知, 因R1不变,R2变大,故R总 将变大;再由总电路纵向关系可知,R总变大,U总不变,故I将变小(电流表读数);因串联电路电流相等I1=I;再由有关R1纵向关系可知,I1变小,R1不变,故U 1将变小(电压表读数变小)。
 爱华网
爱华网