二年级奥数第二十一讲习题及答案:七座桥问题
1.学习欧拉,先将过桥问题转化为一笔画问题,再进行判断(见下图).
过桥问题:
可否一次通过的桥(每座桥只能走一次)?
例:
仿此例依次判断出:
2.下图是乡间的一条小河,上面建有六座桥,你能一次不重复地走遍所有的小桥吗?
(每座小桥最多只准走一次,陆地上可以重复地来回走)
3.在我国著名数学家陈景润写的《数学趣谈》一书中,有下面的这样一道题,大意是说:在法国的首都巴黎有一条河,河中有两个小岛,那里的人们建了15座桥把两个小岛和河岸连接起来,如下图所示,请你说一说,从任一岸出发,一次连续地通过所有的桥到达另一岸,可能吗?(每座桥只能走一次)
4.下图所示为一座售货厅.问顾客从入口进去时,能够一次不重复地走遍各个门吗?请说明你的理由.
如果售厅出口在4号房间由你设计再开一个门,使顾客从入口进去后一次不重复地走遍各个门,再从4号房间出售厅,你打算在哪里再开一个门?
习题解答
1.解:见下图
过桥问题:
可否一次通过所有的桥
(每座桥只能走一次)
一笔画问题:
可否一笔画成图形(笔不能抬起,不能重复)
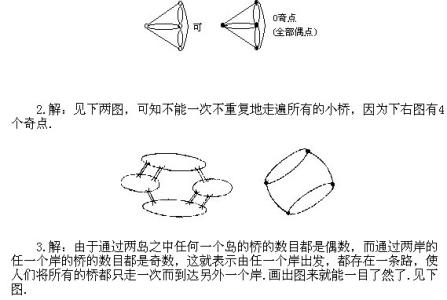
2.解:见下两图,可知不能一次不重复地走遍所有的小桥,因为下右图有4个奇点.
3.解:由于通过两岛之中任何一个岛的桥的数目都是偶数,而通过两岸的任一个岸的桥的数目都是奇数,这就表示由任一个岸出发,都存在一条路,使人们将所有的桥都只走一次而到达另外一个岸.画出图来就能一目了然了.见下图.
因为图中共有两个奇点,且奇点均为岸,是一笔画.
所以人们可以一次通过所有的桥,每座桥只走一次,由一岸到另一岸.
4.解:从入口进入售货厅后,也就是从1号房间开始不能一次不重复地走遍各个门,因为虽然整个图形(见下图)只有2个奇点,但点1是偶点.
当出口在4号房间时,如再在1号和3号房间之间开一个门,则从1号房间开始后就能一次不重复地走遍各个门.因为点1变成了奇点,点4仍为奇点,而整个图形只有2个奇点,因此可以从1号房间进,4号房间出.见下图(进入售货厅后先从1号房间进入3号房间即可).
 爱华网
爱华网



