有几天没更新文章了,最近有些学生问了这样一个问题:梳理好的知识,怎样算是自己基本掌握了?
其实但凡有梳理意识的学生,多多少少都有这样的疑问,这个疑问往往与长时间的被动学习脱不了关系。
在这里不妨预设一个标准:由点推演到面,有面顺理到点的意思无错阐述,就是知识掌握的标准。
学生学习需要用学生的心态去学习知识,用老师的姿态去掌握应用知识。要学会用推演的方式去掌握知识。
管窥一豹而知全身,这是对于基础掌握的基本要求。如果自己连所学是什么,在大脑中都没有清晰的印象,想要做到学习上的胸有成竹是不可能的。
下面,就来教大家一下推演的两种角度:为了方便大多数学生的理解,就以初中数学为例
1.正向视角,由面及点
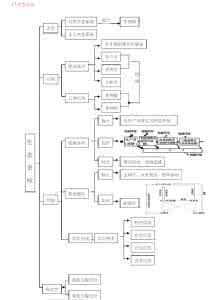
初中数学所有章节的内容,都在这四大体系内,再难超不过这个纲。关键是对这一体系的驾驭能力,决定了自己在数学科目上的信心。我对每一个辅导的学生都会说这样一句话:不管你现在的数学成绩如何,50也好,90是也罢,你的目标都要是满分,最次也要接近满分。
而自己所要做的学习任务无非就是:稳固认知框架,细节拓展到知识点,通过练习定位每一个知识点,熟悉知识点的常规应用,进而形成知识点的深度理解。知识体系框架牢固,知识点能做到深度理解,在数学上有什么理由考不了高分。
而现实中的问题就在于:学生只知道练,知识体系不牢固,熟悉的知识点非常牢固,稍一综合,懵了。
2.反向视角,由点及面
我们通过一道错题,就可以做到有点及面的复习。
要想证明三角和是180°,联想所有的180°知识点:
1.角两边在一条直线上;
2.平行线的同旁内角互补;
3.外角与内角和。
用3,不知内角和是180°,不能证明;用2,可行,答案解出;用1,确保直线划分的3个角对应相等,也能得出辅助线是平行线。
接下来自己想复习,不管从哪一个知识点复习,都能由点及面:
大方向(初中三年章节):
比如从三角形内角和等于180°→三角形章节→平面→平面与立体(由点及面)→线面体和图形缩放→…….
小方向(本章节)
三角形内角和等于180°→三角形性质→三角形(由点及面)→三角形定义→三边关系→分类(边、角)→三角形性质→三角形中特殊的线(高线,中线,角平分线)及特殊的点(垂心,重心,内心)→对边形的内角和
这就是对知识的驾驭能力,而这种驾驭不是天生的,是长期练习后的结果。所以要想做到这样的统御能力,看似很难,但是细细一拆解,就一点都不难了。
STEP1:由梳理的意识进而产生梳理的行为(体系化)
STEP2:由掌握的意识进而产生复习的行为(熟练化)
STEP3:由定位的意识进而产生先定位再解题的习惯(应用化)
随着自己每个章节都用这三步,就可以做到对章节内的知识驾驭能力。
而章节与章节之间产生驾驭能力的方法,除了用我上面提到的归纳法外,还需要用步骤4。
STEP4:由应用意识进而产生错题的查漏补缺(完善整个体系)
总结
学习的点面推演不仅仅适用于数学,还适用于除英语和语文学科之外的其他学科,是学习所有科目学习任务中,最有意思的一个过程,不仅能让知识更牢靠的印入脑海,还能够对知识形成灵活的调用和创新的认知。
关于这一点,是涉及到了学习方法的核心,我会在微信平台里面配一个语音辅助,至于自己感悟到多少,自己有多少收获,取决于自己对于这一块内容的理解、思考和执行。
文章为原创,观点的提出角度是对学习深层次的剖析。 更多学习方法深度剖析的细节文章,每篇文章都有语音辅助,关注“福聿学习之道辅导” 公众平台(微信平台号:tianji_365)找到对应文章即可,如有疑惑或者经验交流,加微信juece365交流哦!
 爱华网
爱华网


