Fuleidehuomu jifen fangcheng
弗雷德霍姆积分方程
Fredholm integral equation
形如
[219-01] (1)和 [219-02] (2)的积分方程,依次称为第一种弗雷德霍姆积分方程和第二种弗雷德霍姆积分方程,其中 是参数,()是未知函数,核(,)和自由项 ()是预先给定的函数。通常假设 (,)属于平方绝对可积函数类,记[219-03][219-18],是非负数。当()恒为零时,称为齐次积分方程,否则称为非齐次积分方程。
逐次逼近法及解核 第二种弗雷德霍姆积分方程的最简便的一种解法是逐次逼近法,即按递推公式
[219-04]给出方程(2)的+1次近似解
[219-05],这里(,)表示(,)的次叠核,即
[219-06]易知,
[219-07],这里可取为小于的任何自然数。当||(时,近似解序列{()}在[,]上是一致收敛的,其极限()就是方程(2)的解。
若级数[219-08]一致收敛,记之为Γ(,;),则Γ(,;)同时满足下面两个方程:
[219-09], (3)
[219-10], (4)对于某值,若有平方绝对可积函数Γ(,;)同时适合方程(3)、(4),则称Γ(,;)为解核。这时方程(2)对任意的自由项()有惟一解,它可表为
[219-11], (5)反之亦然。
对于解核不存在的值 ,称为特征值。否则,称为正则值。当且仅当是特征值时,对应的齐次方程
[219-12] (6)才有非零解。非零解()称为对应于的特征函数。
弗雷德霍姆方法 E.I.弗雷德霍姆给出了一般情形的解核构造法。设 K(,)是有界核,即│(,)│( 是实常数),记
[219-13], (7)
[219-14] , (8)式中
[219-15]
[219-16] 。应用阿达马引理可估计[219-17],从而推知级数(7)、(8)对于一切复值 是绝对一致收敛的,因此,()、(,;)都是关于的整函数,并分别称为弗雷德霍姆行列式和弗雷德霍姆一阶子式。可以证明,解核可表为(,;)=(,;)/()。这表明解核是的半纯函数。同时,解核的极点都是 ()的零点,也都是齐次方程(6)的特征值。反之亦然。
弗雷德霍姆定理 弗雷德霍姆对于第二种积分方程的研究,可归结为如下的四个定理,总称为弗雷德霍姆定理。它是弗雷德霍姆积分方程理论的基础。
第一定理 在复平面的任意有限区域内,方程(2)至多只有有限个特征值。
第二定理 每个特征值λ至少对应于一个特征函数,且所对应的线性无关的特征函数的个数是有限的。这个有限数称为的秩。
第三定理 设是核(,)的特征值,则 是共轭核 [220-01]的特征值。齐次方程 (6)与其共轭齐次方程[220-02]具有相同的秩。
第四定理 若是核(,)的特征值,则非齐次方程(2)可解的充分必要条件为:方程(2)的自由项()与其共轭齐次方程的所有线性无关解()正交,即
[220-03],式中是的秩。
因此,非齐次方程(2),或者对任意自由项可解,或者相应的齐次方程有非零解。这一结论通常称为弗雷德霍姆备择定理。
对于第一种弗雷德霍姆积分方程,若()是它的解,又有非零的任意函数()使得[220-04],则()+()也是它的解。E.施密特对方程(1)的特征值和特征函数给出了如下的定义:若对于某实数 存在非零的函数()和(),满足方程组
[220-05],
[220-06],则称是方程(1)的特征值,而[ (),()]称为对应于的相伴特征函数对。易知,()和()又分别为下面的第二种弗雷德霍姆积分方程的特征函数:
[220-07],式中 [220-08];
[220-09],式中 [220-10]。而(,)(=1,2)都是对称正核,故是实数,不妨认为 > 0。方程(1)一定存在一组正特征值{}和对应的正交标准的相伴特征函数对{(),()}有时也称之为奇值和奇值函数序列。应用它可类似地建立展开定理。施密特指出,方程(1)可解的必要条件是级数[220-11]式中=(,)。以后,.皮卡'" class=link>(C.-).皮卡进而证明,在正交标准特征函数系{()}是完备的情形,这条件也是充分的。此即所谓施密特-皮卡定理。
对于第一种弗雷德霍姆积分方程的研究,近代有了新的进展,并提供了一些有效的解法,但至今还未建立起系统的理论。
李明忠
以上就是网友分享的关于"弗雷德霍姆积分方程"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
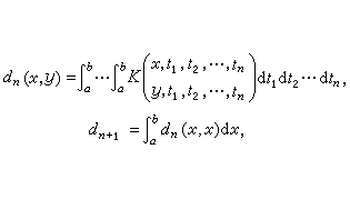
 爱华网
爱华网


